搜索
【题目】如图1，已知
，
平分
．
（1）
；
（2）若在图1中画射线
，设
，
平分
，用含
的代数式表示
的大小；
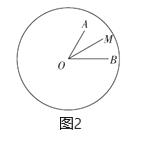
（3）如图2，若线段
与
分别为同一钟表上某一时刻的时针与分针，，在时针与分针转动过程中，始终平分，则经过多少时间后，
的度数第一次等于
．
参考答案：
【答案】（1）
；（2）
或
或
；（3）
.
【解析】
（1）根据角平分线的定义，即可求解；
（2）分3种情况：①当
在
下方时，②当在上方且
时，③当在上方且
时，分别求解即可；
（3）设经过
分钟，
的度数第一次等于
，根据等量关系，列出关于t的方程，即可求解.
（1）∵
，
平分
．
∴
=×60°=.
故答案是：；
（2）①当在下方时，
；
②当在上方且时，
；
③当在上方且时，
；
（3）∵
，平分，
∴
.
设经过分钟，的度数第一次等于，
根据题意得：
，
解得：
∴经过分钟，的度数第一次等于.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某农户承包荒山若干亩，种果树2000棵．今年水果总产量为18000千克，此水果在市场上每千克售
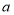元，在果园每千克售
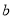元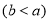
．该农户将水果拉到市场出售平均每天出售1000千克，需8人帮忙，每人每天付工资25元，农用车运费及其他各项税费平均每天100元．（1）分别用
表示两种方式出售水果的收入．（2）若
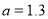元，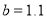
元，且两种方式都在相同的时间内售完全部水果，请你通过计算说明选择哪种出售方式较好． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图在平行四边形ABCD中，CD＝2AD，BE⊥AD，点F为DC中点，连接EF、BF，下列结论：①∠ABC＝2∠ABF；②EF＝BF；③S四边形DEBC＝2S△EFB；④∠CFE＝3∠DEF，其中正确的有_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解题
阅读材料：
两个两位数相乘，如果这两个因数的十位数字相同，个位数字的和是10，该类乘法的速算方法是：将一个因数的十位数字与另一个因数的十位数字加1的和相乘，所得的积作为计算结果的前两位，将两个因数的个位数字之积作为计算结果的后两位（数位不足两位，用0补齐）。
比如
，它们乘积的前两位是
，它们乘积的后两位是
，所以
；再如
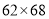，它们乘积的前两位是
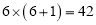，它们乘积的后两位是
，所以
；又如
，
，不足两位，就将6写在百位：
，不足两位，就将9写在个位，十位上写0，所以
该速算方法可以用我们所学的整式乘法与分解因式的知识说明其合理性；
设其中一个因数的十位数字为
，个位数字是
，（、表示1~9的整数），则该数可表示为
，另一因数可表示为
．两数相乘可得：
.（注：其中
表示计算结果的前两位，
表示计算结果的后两位。）问题：
两个两位数相乘，如果其中一个因数的十位数字与个位数字相同，另一因数的十位数字与个位数字之和是10．
如
、
、
等．（1）探索该类乘法的速算方法，请以
为例写出你的计算步骤；（2）设十位数字与个位数字相同的因数的十位数字是
，则该数可以表示为___________．设另一个因数的十位数字是
，则该数可以表示为___________．（、表示1~9的正整数）（3）请针对问题（1）（2）中的计算，模仿阅读材料中所用的方法写出如：
的运算式：____________________ -
科目： 来源： 题型：
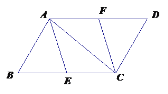
查看答案和解析>>【题目】已知：如图，在□ABCD中，E、F分别为BC、AD的中点．
（1）试判断四边形AECF是什么四边形？为什么？
（2）当AB⊥AC时，四边形AECF是什么四边形？
（3）结合图形，请你添加一个条件，使其与原已知条件共同能推出四边形AECF是矩形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用黑、白正方形按如图规律排列．
(1)第10个和第11图形中，黑色正方形各有多少个？
(2)找出图形变化的规律，说明第n个图形中黑色正方形的个数与n的关系．
(3)这列图形中，是否存在黑色正方形的个数为2019的图形？
-
科目： 来源： 题型：
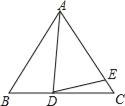
查看答案和解析>>【题目】已知△ABC，AB＝AC，D为BC上一点，E为AC上一点，AD＝AE．
（1）如果∠BAD＝10°，∠DAE＝30°，那么∠EDC＝ °．
（2）如果∠ABC＝60°，∠ADE＝70°，那么∠BAD＝ °，∠CDE＝ °．
（3）设∠BAD＝α，∠CDE＝β猜想α，β之间的关系式，并说明理由．
相关试题
