【题目】如图在平行四边形ABCD中,CD=2AD,BE⊥AD,点F为DC中点,连接EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确的有_____.

参考答案:
【答案】①②③④
【解析】
延长EF交BC的延长线于G,取AB的中点H连接FH.想办法证明EF=FG,BE⊥BG,四边形BCFH是菱形即可解决问题.
如图延长EF交BC的延长线于G,取AB的中点H连接FH.

∵CD=2AD,DF=FC,
∴CF=CB,
∴∠CFB=∠CBF,
∵CD∥AB,
∴∠CFB=∠FBH,
∴∠CBF=∠FBH,
∴∠ABC=2∠ABF.故①正确,
∵DE∥CG,
∴∠D=∠FCG,
∵DF=FC,∠DFE=∠CFG,
∴△DFE≌△FCG(AAS),
∴FE=FG,
∵BE⊥AD,
∴∠AEB=90°,
∵AD∥BC,
∴∠AEB=∠EBG=90°,
∴BF=EF=FG,故②正确,
∵S△DFE=S△CFG,
∴S四边形DEBC=S△EBG=2S△BEF,故③正确,
∵AH=HB,DF=CF,AB=CD,
∴CF=BH,∵CF∥BH,
∴四边形BCFH是平行四边形,
∵CF=BC,
∴四边形BCFH是菱形,
∴∠BFC=∠BFH,
∵FE=FB,FH∥AD,BE⊥AD,
∴FH⊥BE,
∴∠BFH=∠EFH=∠DEF,
∴∠EFC=3∠DEF,故④正确,
故答案为:①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使得△MNP为等腰直角三角形,则符合条件的点P有(提示:直角三角形斜边上的中线等于斜边的一半)( )

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB,反向延长线段AB到C,使BC=
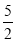 AB,D为BC的中点,E为BD的中点.
AB,D为BC的中点,E为BD的中点.(1)①补全图形;
②若AB=4,则AE=_____(直接写出结果).
(2)若AE=2,求AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户承包荒山若干亩,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售
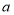 元,在果园每千克售
元,在果园每千克售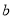 元
元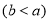 .该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
.该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.(1)分别用
 表示两种方式出售水果的收入.
表示两种方式出售水果的收入.(2)若
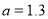 元,
元,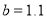 元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题
阅读材料:
两个两位数相乘,如果这两个因数的十位数字相同,个位数字的和是10,该类乘法的速算方法是:将一个因数的十位数字与另一个因数的十位数字加1的和相乘,所得的积作为计算结果的前两位,将两个因数的个位数字之积作为计算结果的后两位(数位不足两位,用0补齐)。
比如
 ,它们乘积的前两位是
,它们乘积的前两位是 ,它们乘积的后两位是
,它们乘积的后两位是 ,所以
,所以 ;
;再如
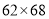 ,它们乘积的前两位是
,它们乘积的前两位是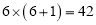 ,它们乘积的后两位是
,它们乘积的后两位是 ,所以
,所以 ;
;又如
 ,
, ,不足两位,就将6写在百位:
,不足两位,就将6写在百位: ,不足两位,就将9写在个位,十位上写0,所以
,不足两位,就将9写在个位,十位上写0,所以
该速算方法可以用我们所学的整式乘法与分解因式的知识说明其合理性;
设其中一个因数的十位数字为
 ,个位数字是
,个位数字是 ,(
,( 、
、 表示1~9的整数),则该数可表示为
表示1~9的整数),则该数可表示为 ,另一因数可表示为
,另一因数可表示为 .
.两数相乘可得:




 .
.(注:其中
 表示计算结果的前两位,
表示计算结果的前两位, 表示计算结果的后两位。)
表示计算结果的后两位。)问题:
两个两位数相乘,如果其中一个因数的十位数字与个位数字相同,另一因数的十位数字与个位数字之和是10.
如
 、
、 、
、 等.
等.(1)探索该类乘法的速算方法,请以
 为例写出你的计算步骤;
为例写出你的计算步骤;(2)设十位数字与个位数字相同的因数的十位数字是
 ,则该数可以表示为___________.
,则该数可以表示为___________.设另一个因数的十位数字是
 ,则该数可以表示为___________.(
,则该数可以表示为___________.( 、
、 表示1~9的正整数)
表示1~9的正整数)(3)请针对问题(1)(2)中的计算,模仿阅读材料中所用的方法写出如:
 的运算式:____________________
的运算式:____________________ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
 ,
, 平分
平分 .
.(1)
 ;
;(2)若在图1中画射线
 ,设
,设 ,
, 平分
平分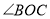 ,用含
,用含 的代数式表示
的代数式表示 的大小;
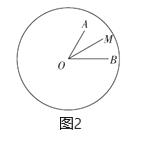
的大小;(3)如图2,若线段
 与
与 分别为同一钟表上某一时刻的时针与分针,
分别为同一钟表上某一时刻的时针与分针, ,在时针与分针转动过程中,
,在时针与分针转动过程中, 始终平分
始终平分 ,则经过多少时间后,
,则经过多少时间后, 的度数第一次等于
的度数第一次等于 .
.

-
科目: 来源: 题型:
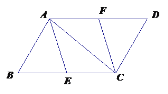
查看答案和解析>>【题目】已知:如图,在□ABCD中,E、F分别为BC、AD的中点.
(1)试判断四边形AECF是什么四边形?为什么?
(2)当AB⊥AC时,四边形AECF是什么四边形?
(3)结合图形,请你添加一个条件,使其与原已知条件共同能推出四边形AECF是矩形.
相关试题

