搜索
【题目】如图，已知B、C两点把线段AD分成2：4：3的三部分，M是AD的中点，若CD=6，求：
（1）线段MC的长．
（2）AB：BM的值．
参考答案：
【答案】(1)3(2)4:5
【解析】试题分析：（1）AB:BC:CD=2:4:3，可得线段
、线段
的长，根据线段的和差，可得线段
的长，根据线段中点的性质，可得
的长，根据线段的和差，可得答案；
（2）根据线段中点的性质，可得
的长，根据线段的和差，可得
的长，根据比的意义，可得答案．
试题解析：(1)由AB:BC:CD=2:4:3，CD=6，得
AB=4，BC=8.
由线段的和差，得
AD=AB+BC+CD=4+8+6=18.
由线段中点的性质，得
由线段的和差，得
MC=MDCD=96=3；
(2)由线段的和差，得
BM=AMAB=94=5.
由比的意义，得
AB:BM=4:5.
-
科目： 来源： 题型：
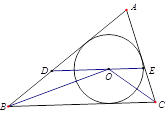
查看答案和解析>>【题目】如图，⊙O是△ABC的内切圆，过点O作DE∥BC，与AB、AC分别交于点D、E.
（1）求证：BD+CE＝DE；
（2）若∠BAC=70，求∠BOC的度数
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，池塘边有块长为20m，宽为10m的长方形土地，现在将其余三面留出宽都是xm的小路，中间余下的长方形部分做菜地，用含x的式子表示：
（1）菜地的长a= m，菜地的宽b= m；菜地的周长C= m；
（2）求当x=1m时，菜地的周长C．
-
科目： 来源： 题型：
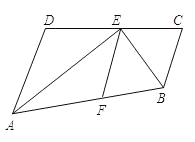
查看答案和解析>>【题目】如图，点E在线段CD上，EA、EB分别平分∠DAB和∠CBA,点F在线段AB上运动，AD=4cm，BC=3cm，且AD∥BC.
（1）你认为AE和BE有什么位置关系？并验证你的结论；
（2）当点F运动到离点A多少厘米时，△ADE和△AFE全等？为什么？
（3）在（2）的情况下，此时BF=BC吗？证明你的结论并求出AB的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=ax+b的图像与正比例函数y=kx的图像交于点M，
（1）求正比例函数和一次函数的解析式；
（2）根据图像写出使正比例函数的值大于一次函数的值的x的取值范围；
（3）求ΔMOP的面积。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于A（﹣2，0），B（4，0）两点，顶点C到x轴的距离为2，则此抛物线的解析式为______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面解答过程，并填空或填理由．
已知如下图，点E、F分别是AB和CD上的点，DE、AF分别交BC于点G、H，∠A=∠D，∠1=∠2．
试说明：∠B=∠C．
解：∵∠1=∠2（已知）
∠2=∠3（___________）
∴∠3=∠1（等量代换）
∴AF∥DE（___________）
∴∠4=∠D（___________）
又∵∠A=∠D（已知）
∴∠A=∠4（等量代换）
∴AB∥CD（___________）
∴∠B=∠C（___________）．
相关试题
