【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中: ①△ABC≌△EAD;
②△ABE是等边三角形;
③AD=AF;
④S△ABE=S△CDE;
⑤S△ABE=S△CEF .
其中正确的是( )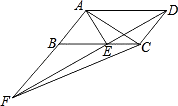
A.①②③
B.①②④
C.①②⑤
D.①③④
参考答案:
【答案】C
【解析】解:∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC,
∴∠EAD=∠AEB,
又∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形;②正确;
∴∠ABE=∠EAD=60°,
∵AB=AE,BC=AD,
∴△ABC≌△EAD(SAS);①正确;
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),
∴S△FCD=S△ABC ,
又∵△AEC与△DEC同底等高,
∴S△AEC=S△DEC ,
∴S△ABE=S△CEF;⑤正确.
若AD与AF相等,即∠AFD=∠ADF=∠DEC
即EC=CD=BE
即BC=2CD,
题中未限定这一条件
∴③④不一定正确;
故选C.
【考点精析】本题主要考查了等边三角形的判定和平行四边形的性质的相关知识点,需要掌握三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在反比例函数
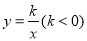 上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8。
上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8。(1)求证:△EOB∽△ABC;
(2)求反比例函数的解析式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果平行四边形ABCD被一条对角线分成两个等腰三角形,则称该平行四边形为“等腰平行四边形”,如果等腰平行四边形ABCD的一组邻边长分别为4和6,则它的面积是( )
A.16 或6
或6 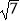
B.8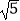 或6
或6 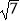
C.16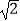
D.8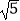
-
科目: 来源: 题型:
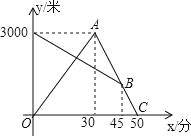
查看答案和解析>>【题目】某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
(1)求张强返回时的速度;
(2)妈妈比按原速返回提前多少分钟到家?
(3)请直接写出张强与妈妈何时相距1000米?
-
科目: 来源: 题型:
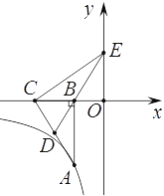
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与x轴相交于点A(-2,0),与y轴交于点C,与反比例函数
 在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.(1)求一次函数的表达式;
(2)求反比例函数的表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】合肥市某日的气温是﹣2℃~6℃,则该日的温差是( )
A.8℃B.5℃C.2℃D.﹣8℃
相关试题

