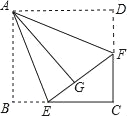
【题目】如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
(1)求证:四边形ABCD是正方形;
(2)求证:三角形ECF的周长是四边形ABCD周长的一半;
(3)若EC=FC=1,求AB的长度.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() +1
+1
【解析】分析:(1)由题意得,∠BAE=∠EAG,∠DAF=∠FAG,于是得到∠BAD=2∠EAF=90°,推出四边形ABCD是矩形,根据正方形的判定定理即可得到结论;
(2)根据EG=BE,FG=DF,得到EF=BE+DF,于是得到△ECF的周长=EF+CE+CF=BE+DF+CE+CF=BC+CD,即可得到结论;
(3)根据EC=FC=1,得到BE=DF,根据勾股定理得到EF=![]() ,于是得到结论.
,于是得到结论.
详(1)证明:由题意得,∠BAE=∠EAG,∠DAF=∠FAG,
∴∠BAD=2∠EAF=90°,
∴四边形ABCD是矩形,
∵AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
(2)证明:∵EG=BE,FG=DF,
∴EF=BE+DF,
∴△ECF的周长=EF+CE+CF=BE+DF+CE+CF=BC+CD,
∴三角形ECF的周长是四边形ABCD周长的一半;
(3)∵EC=FC=1,
∴BE=DF,
∴EF=![]() ,
,
∵EF=BE+DF,
∴BE=DF=![]() EF=
EF=![]() ,
,
∴AB=BC=BE+EC=![]() +1.
+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示的是带支架功能的某品牌手机壳,将其侧面抽象为如图2所示的几何图形,已知AB=5cm,∠BAC=60°,∠C=45°,则AC的长(
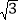 ≈1.732,结果精确到0.1cm)为( )
≈1.732,结果精确到0.1cm)为( )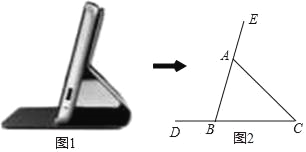
A. 3.4cm B. 4.6cm C. 5.8cm D. 6.8cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )

A. 30
 m B. 20
m B. 20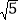 m C. 30
m C. 30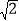 m D. 15
m D. 15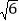 m
m -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图:在△ABC中,AC=3,BC=6,∠C=60
 ;
;(1)将△ABC绕着点C旋转,使点A落在直线BC上的点A′,点B落在B′,在下图中画出旋转后的△A′B′C.
(2)直接写出A′B的长,A′B=___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为
 ,连接CF,则CF= .
,连接CF,则CF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科普小组有5名成员,身高(单位:cm)分别为:160,165,170,163,172,把身高160 cm的成员替换成一位165 cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
A.平均数变小,方差变小B.平均数变大,方差变大
C.平均数变大,方差不变D.平均数变大,方差变小
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明想用镜子测量一棵松树的高度,但树旁有一条河,不能测量镜子与树之间的距离,于是小明两次利用镜子,第一次他把镜子放在C点,人在F点正好在镜子中看见树尖A;第二次把镜子放在D点,人在H点正好在镜子中看到树尖A.已知小明的眼睛距离地面的距离EF=1.68米,量得CD=10米,CF=1.2米,DH=3.6米,利用这些数据你能求出这棵松树的高度吗?试试看.(友情提示:∠ACB=∠ECF,∠ADF=∠GDH)

相关试题

