【题目】某中学对“希望工程捐款活动”进行抽样调查,得到一组学生捐款情况的数据![]() 如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8,又知此次调查中捐15元和20元的人数共39人.
如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8,又知此次调查中捐15元和20元的人数共39人.
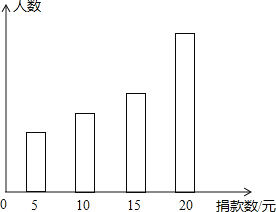
![]() 他们一共抽查了多少人?
他们一共抽查了多少人?
![]() 这组数据的众数、中位数各是多少?
这组数据的众数、中位数各是多少?
![]() 若该校共有1500名学生,请你估算全校学生共捐款多少元?
若该校共有1500名学生,请你估算全校学生共捐款多少元?
参考答案:
【答案】(1)60人;(2)众数为20元;中位数为15元;(3)21750元
【解析】
(1)利用从左到右各长方形高度之比为3:4:5:8,可设捐5元、10元、15元和20元的人数分别为3x、4x、5x、8x,则根据题意得5x+8x=39,解得x=3,然后计算3x+4x+5x+8x即可;
(2)先确定各组的人数,然后根据中位数和众数的定义求解;
(3)先计算出样本的加权平均数,然后利用样本平均数估计总体,用1500乘以样本平均数即可.
解:![]() 设捐5元、10元、15元和20元的人数分别为3x、4x、5x、8x,
设捐5元、10元、15元和20元的人数分别为3x、4x、5x、8x,
![]() ,
,
解得:![]() ,
,
![]() 人
人![]() ;
;
![]() 捐5元、10元、15元和20元的人数分别为9、12、15、24,
捐5元、10元、15元和20元的人数分别为9、12、15、24,
![]() 出现次数最多,
出现次数最多,
∴众数为20元;
![]() 共有60个数据,第30个和第31个数据落在第三组内,
共有60个数据,第30个和第31个数据落在第三组内,
∴中位数为15元;
![]() 元
元![]() ,
,
∴估算全校学生共捐款21750元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线l:y=
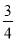 x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y= x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】由线段a,b,c组成的三角形不是直角三角形的是( )
A. a=15,b=8,c=17 B. a=12,b=14,c=15
C. a=
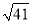 ,b=4,c=5 D. a=7,b=24,c=25
,b=4,c=5 D. a=7,b=24,c=25 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,
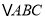 的顶点都在网格点上,其中,C点坐标为
的顶点都在网格点上,其中,C点坐标为 .
.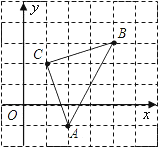
(1)写出点A、B的坐标:
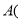 ______ ,______
______ ,______ 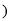 、
、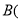 ______ ,______
______ ,______ 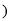
(2)将
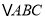 先向左平移2个单位长度,再向上平移1个单位长度,得到
先向左平移2个单位长度,再向上平移1个单位长度,得到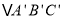 ,则
,则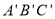 的三个顶点坐标分别是
的三个顶点坐标分别是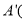 ______ ,______
______ ,______ 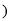 、
、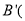 ______ ,______
______ ,______ 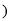 、
、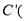 ______ ,______
______ ,______ 
(3)求
 的面积.
的面积. -
科目: 来源: 题型:
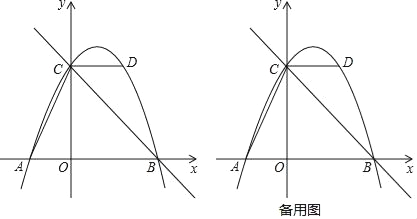
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC、CD.
(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标.
-
科目: 来源: 题型:
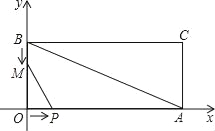
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知矩形OACB的边OA,OB分别在x轴上和y轴上,线段OA=24,OB=12;点P从点O开始沿OA边匀速移动,点M从点B开始沿BO边匀速移动.如果点P,点M同时出发,它们移动的速度相同都是1个单位/秒,设经过x秒时(0≤x≤12),△POM的面积为y.
(1)求直线AB的解析式;
(2)求y与x的函数关系式;
(3)连接矩形的对角线AB,当x为何值时,以M、O、P为顶点的三角形等于△AOB面积的
 ;
;(4)当△POM的面积最大时,将△POM沿PM所在直线翻折后得到△PDM,试判断D点是否在直线AB上,请说明理由.
-
科目: 来源: 题型:
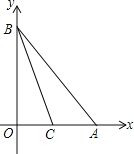
查看答案和解析>>【题目】如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,S△BOC=S△ABC.
(1)求直线BC的解析式;
(2)在直线BC上求作一点P,使四边形OBAP为平行四边形(尺规作图,保留痕迹,不写作法).
相关试题

