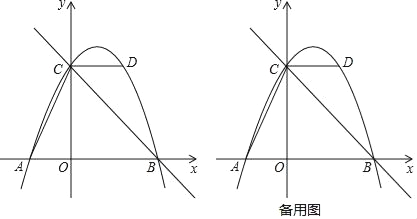
【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC、CD.
(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标.
参考答案:
【答案】(1)y=﹣![]() x2+x+4,(2) 点E的坐标为(1,
x2+x+4,(2) 点E的坐标为(1,![]() ),(3,
),(3,![]() ).
).
【解析】
(1)设抛物线的解析式为y=a(x﹣x1)(x﹣x2),再把点代入即可得出解析式;
(2)分两种情况:①当点E在直线CD的抛物线上方;②当点E在直线CD的抛物线下方;连接CE,过点E作EF⊥CD,再由三角函数得出点E的坐标.
(1)∵抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),
∴设抛物线的解析式为y=a(x﹣x1)(x﹣x2),
∴y=a(x+2)(x﹣4),
∴﹣8a=4,
∴a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() (x+2)(x﹣4)=﹣
(x+2)(x﹣4)=﹣![]() x2+x+4,
x2+x+4,
(2)①当点E在直线CD的抛物线上方,记E′,连接CE′,过点E′作E′F′⊥CD,垂足为F′,
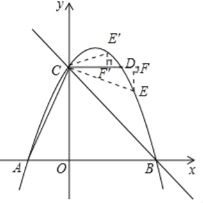
由(1)得OC=4,
∵∠ACO=∠E′OF′,
∴tan∠ACO=tan∠E′CF′,
∴![]() ,
,
设线段E′F′=h,则CF′=2h,
∴点E′(2h,h+4),
∵点E′在抛物线上,
∴﹣![]() (2h)2+2h+4=h+4,
(2h)2+2h+4=h+4,
∴h1=0(舍去),h2=![]() ,
,
∴E′(1,![]() );
);
②当点E在直线CD的抛物线下方;
同①的方法得,E(3,![]() ),
),
综上,点E的坐标为(1,![]() ),(3,
),(3,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】由线段a,b,c组成的三角形不是直角三角形的是( )
A. a=15,b=8,c=17 B. a=12,b=14,c=15
C. a=
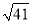 ,b=4,c=5 D. a=7,b=24,c=25
,b=4,c=5 D. a=7,b=24,c=25 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,
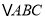 的顶点都在网格点上,其中,C点坐标为
的顶点都在网格点上,其中,C点坐标为 .
.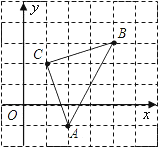
(1)写出点A、B的坐标:
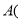 ______ ,______
______ ,______ 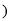 、
、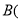 ______ ,______
______ ,______ 
(2)将
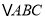 先向左平移2个单位长度,再向上平移1个单位长度,得到
先向左平移2个单位长度,再向上平移1个单位长度,得到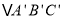 ,则
,则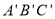 的三个顶点坐标分别是
的三个顶点坐标分别是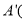 ______ ,______
______ ,______ 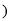 、
、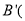 ______ ,______
______ ,______ 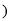 、
、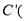 ______ ,______
______ ,______ 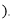
(3)求
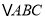 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对“希望工程捐款活动”进行抽样调查,得到一组学生捐款情况的数据
 如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8,又知此次调查中捐15元和20元的人数共39人.
如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8,又知此次调查中捐15元和20元的人数共39人.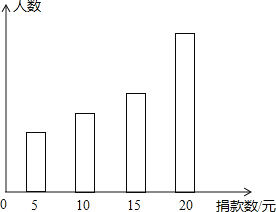
 他们一共抽查了多少人?
他们一共抽查了多少人? 这组数据的众数、中位数各是多少?
这组数据的众数、中位数各是多少? 若该校共有1500名学生,请你估算全校学生共捐款多少元?
若该校共有1500名学生,请你估算全校学生共捐款多少元? -
科目: 来源: 题型:
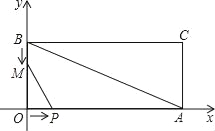
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知矩形OACB的边OA,OB分别在x轴上和y轴上,线段OA=24,OB=12;点P从点O开始沿OA边匀速移动,点M从点B开始沿BO边匀速移动.如果点P,点M同时出发,它们移动的速度相同都是1个单位/秒,设经过x秒时(0≤x≤12),△POM的面积为y.
(1)求直线AB的解析式;
(2)求y与x的函数关系式;
(3)连接矩形的对角线AB,当x为何值时,以M、O、P为顶点的三角形等于△AOB面积的
 ;
;(4)当△POM的面积最大时,将△POM沿PM所在直线翻折后得到△PDM,试判断D点是否在直线AB上,请说明理由.
-
科目: 来源: 题型:
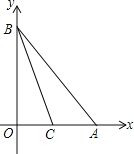
查看答案和解析>>【题目】如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,S△BOC=S△ABC.
(1)求直线BC的解析式;
(2)在直线BC上求作一点P,使四边形OBAP为平行四边形(尺规作图,保留痕迹,不写作法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,抛物线y=mx2﹣2m2x+2交y轴于A点,交直线x=4于B点.
(1)抛物线的对称轴为x=_____(用含m的代数式表示);
(2)若AB∥x轴,求抛物线的表达式;
(3)记抛物线在A,B之间的部分为图象G(包含A,B两点),若对于图象G上任意一点P(xp,yp),yp≤2,求m的取值范围.
相关试题

