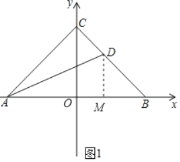
【题目】如图,在直角坐标系中,△ABC的三个顶点都在坐标轴上,A,B两点关于y轴对称,点C是y轴正半轴上一个动点,AD是角平分线.
(1)如图1,若∠ACB=90°,直接写出线段AB,CD,AC之间数量关系;
(2)如图2,若AB=AC+BD,求∠ACB的度数;
(3)如图2,若∠ACB=100°,求证:AB=AD+CD.

参考答案:
【答案】(1)AB=AC+CD;(2)108°;(3)证明见解析
【解析】
(1)如图1,过D作DM⊥AB于M,根据轴对称的性质得到CA=CB,根据角平分线的性质得到CD=MD,∠ABC=45°,根据全等三角形的性质得到AC=AM,于是得到结论;
(2)设∠ACB=α,则∠CAB=∠CBA=90°-![]() α,在AB上截取AK=AC,连结DK,根据角平分线的定义得到∠CAD=∠KAD,根据全等三角形的性质得到∠ACD=∠AKD=α,根据三角形的内角和即可得到结论;
α,在AB上截取AK=AC,连结DK,根据角平分线的定义得到∠CAD=∠KAD,根据全等三角形的性质得到∠ACD=∠AKD=α,根据三角形的内角和即可得到结论;
(3)如图2,在AB上截取AH=AD,连接DH,根据等腰三角形的性质得到∠CAB=∠CBA=40°,根据角平分线的定义得到∠HAD=∠CAD=20°,求得∠ADH=∠AHD=80°,在AB上截取AK=AC,连接DK,根据全等三角形的性质得到∠ACB=∠AKD=100°,CD=DK,根据等腰三角形的性质得到DH=BH,于是得到结论.
(1)如图1,过D作DM⊥AB于M,
∵A,B两点关于y轴对称,
∴CA=CB,
∵∠ACB=90°,AD是角平分线,
∴CD=MD,∠ABC=45°,
∴∠BDM=45°,
∴BM=DM,
∴BM=CD,
在RT△ADC和RT△ADM中,![]() ,
,
∴RT△ADC≌RT△ADM(HL),
∴AC=AM,
∴AB=AM+BM=AC+CD,
即AB=AC+CD;
(2)设∠ACB=α,则∠CAB=∠CBA=90°﹣![]() α,
α,
在AB上截取AK=AC,连结DK,
∵AB=AC+BD,
∴BK=BD,
∵AD是角平分线,
∴在△CAD和△KAD中,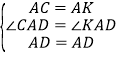 ,
,
∴△CAD≌△KAD(SAS),
∴∠ACD=∠AKD=α,
∴∠BKD=180°﹣α,
∵BK=BD,
∴∠BDK=180°﹣α,
在△BDK中,
180°﹣α+180°﹣α+90°﹣![]() α=180°,
α=180°,
∴α=108°,
∴∠ACB=108°;
(3)如图2,在AB上截取AH=AD,连接DH,
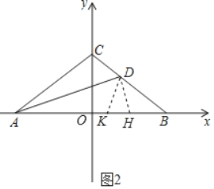
∵∠ACB=100°,AC=BC,
∴∠CAB=∠CBA=40°,
∵AD是角平分线,
∴∠HAD=∠CAD=20°,
∴∠ADH=∠AHD=80°,
在AB上截取AK=AC,连接DK,
由(1)得,△CAD≌△KAD,
∴∠ACB=∠AKD=100°,CD=DK,
∴∠DKH=80°=∠DHK,
∴DK=DH=CD,
∵∠CBA=40°,
∴∠BDH=40°,
∴DH=BH,
∴BH=CD,
∵AB=AH+BH,
∴AB=AD+CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两条高AD,BE交于点F,∠ABC=45°,∠BAC=60°.
(1)求证:DF=DC;
(2)连接CF,求证:AB=AC+CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
小聪在解方程组
 时,发现方程组中①和②之间存在一定的关系,他发现了一种“整体代换”法,具体解法如下:
时,发现方程组中①和②之间存在一定的关系,他发现了一种“整体代换”法,具体解法如下:解:将方程②变形为:

即

把方程①代入方程③得:
 解得
解得
把
 代入方程①得
代入方程①得
∴方程组的解是

(1)模仿小聪的解法,解方程组

(2)已知x,y满足方程组
 ,解答:
,解答:(ⅰ)求
 的值;
的值; (ⅱ)求
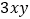 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形ABCD的顶点A(a,0),B(b,0)在坐标轴上,C的纵坐标是2,且a,b满足式子:

(1)求出点A、B、C的坐标.
(2)连接AC,在y轴上是否存在点M,使△COM的面积等于△ABC的面积,若存在请求出点M的坐标,若不存在请说明理由.
(3)若点P是边CD上一动点,点Q是CD与y轴的交点,连接OP,OE平分∠AOP交直线CD于点E,OF⊥OE交直线CD于点F,当点P运动时,探究∠OPD和∠EOQ之间的数量关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图中阴影部分的面积为( )

A.1
B.2
C.1+
D.2﹣
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有个点
 ,点
,点 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点 ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点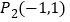 ,第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第200次跳动至点
,第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第200次跳动至点 的坐标是( )
的坐标是( )
A. (51,100)B. (50,100)C. (-50,100)D. (-51,100)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.


相关试题

