【题目】如图,在锐角△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.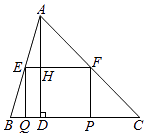
(1)求证: ![]() =
= ![]() ;
;
(2)设EF的长为x.
①当x为何值时,矩形EFPQ为正方形?
②当x为何值时,矩形EFPQ的面积最大?并求其最大值.
参考答案:
【答案】
(1)
解:证明:∵四边形EFPQ是矩形,
∴EF∥BC,
∴△AEF∽△ABC,∠AHF=∠ADC,
又∵AD是高,
∴∠AHF=∠ADC=90°,即AH是△AEF的高.
∴ ![]() ;
;
(2)
解:①若矩形EFPQ为正方形,则HD=EQ=EF=x.
∴AH=AD﹣HD=8﹣x.
又∵ ![]() ,BC=10,
,BC=10,
∴ ![]() .
.
解得 ![]() .
.
∴当 ![]() 时,矩形EFPQ为正方形;
时,矩形EFPQ为正方形;
②∵HD=EQ,AD=8,
∴AH=AD﹣HD=8﹣EQ.
又∵ ![]() ,EF=x,BC=10,
,EF=x,BC=10,
∴ ![]() .
.
∴ ![]() .
.
∴S矩形EFPQ= ![]() .
.
∵S矩形EFPQ= ![]() (0<x<10),
(0<x<10),
∴当x=5时,S矩形EFPQ有最大值为20.
∴当x=5时,矩形EFPQ的面积最大,最大面积为20
【解析】(1)根据矩形的性质得出EQ=HD=FP,EF∥BC,推出△AEF∽△ABC,根据相似三角形的性质推出即可;(2)①根据正方形的性质可知HD=EQ=EF,令HD=EQ=EF=x;利用相似三角形的性质可得 ![]() ,可得x的值;②根据矩形的面积公式,可以把面积表示成关于EF的长的函数,根据函数的性质即可求解.
,可得x的值;②根据矩形的面积公式,可以把面积表示成关于EF的长的函数,根据函数的性质即可求解.
【考点精析】掌握关于仰角俯角问题是解答本题的根本,需要知道仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,BC边上的高AD=12,则BC的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是
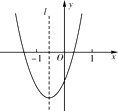
A.a<0
B.c>0
C.a+b+c>0
D.b2-4ac<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB>AC , 分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N , 作直线MN交AB于点D;连结CD.若AB=7,AC=5,则△ACD的周长为( )
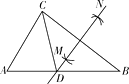
A.2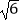
B.12
C.17
D.19 -
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇准备完成题目:化简:
 ,发现系数“
,发现系数“ ”印刷不清楚.
”印刷不清楚.(1)他把“
 ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“
 ”是几?
”是几? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1的⊙O与正五边形ABCDE相切于点A、C , 则弧AC的长为

A. π
π
B. π
π
C. π
π
D. π
π -
科目: 来源: 题型:
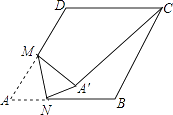
查看答案和解析>>【题目】如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 .
相关试题

