Question

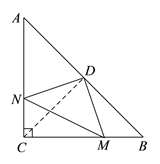
【题目】在△ABC中，∠ACB=90°，AC=BC=4，点D为AB的中点，M，N分别在BC，AC上，且BM=CN现有以下四个结论：

①DN=DM； ② ∠NDM=90°； ③ 四边形CMDN的面积为4； ④△CMN的面积最大为2.

其中正确的结论有（ ）

A. ①②④； B. ①②③； C. ②③④； D. ①②③④.

Answer 1

【答案】D

【解析】连接CD，

∵在△ABC中，∠ACB=90°，AC=BC=4，点D为AB的中点，

∴∠B=∠NCD=45°，CD=BD，∠CDB=90°，S△CDB=S△ABC=·AC·BC==4 ，

又∵BM=CN，

∴△DBM≌△DCN，

∴DN=DM，∠CDN=∠DBM，S△CDN=S△DBM，

∴∠DMN=∠CDN+∠CDM=∠CDM+∠BDM=∠CDB=90°，

S四边形CMDN=S△CDN+S△CDM= S△BDM+S△CDM=S△CBD=4.

∵S△CMN+S△DMN= S四边形CMDN=4，

∴当S△DMN最小时，S△CMN的面积最大，

∴当DM⊥BC时，DM=DN=2，此时S△DMN最小=2，

∴此时，S△CMN的面积最大=4-2=2.

综上所述，上述四个结论全都正确.

故选D.