【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.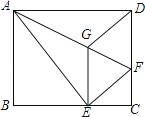
(1)求证:四边形EFDG是菱形;
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2 ![]() ,求BE的长.
,求BE的长.
参考答案:
【答案】
(1)
证明:
∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF.
∴四边形EFDG为菱形
(2)
解:EG2= ![]() GFAF.
GFAF.
理由:如图1所示:连接DE,交AF于点O.
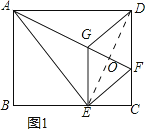
∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF= ![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴ ![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO= ![]() GF,DF=EG,
GF,DF=EG,
∴EG2= ![]() GFAF
GFAF
(3)
解:如图2所示:过点G作GH⊥DC,垂足为H.
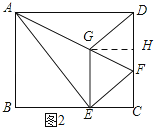
∵EG2= ![]() GFAF,AG=6,EG=2
GFAF,AG=6,EG=2 ![]() ,
,
∴20= ![]() FG(FG+6),整理得:FG2+6FG﹣40=0.
FG(FG+6),整理得:FG2+6FG﹣40=0.
解得:FG=4,FG=﹣10(舍去).
∵DF=GE=2 ![]() ,AF=10,
,AF=10,
∴AD= ![]() =4
=4 ![]() .
.
∵GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴ ![]() ,即
,即 ![]() =
= ![]() .
.
∴GH= ![]() .
.
∴BE=AD﹣GH=4 ![]() ﹣
﹣ ![]() =
= ![]()
【解析】(1)先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF;(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF= ![]() GF,接下来,证明本题主要考查的是四边形与三角形的综合应用,解答本题主要应用了矩形的性质、菱形的判定和性质、相似三角形的性质和判定、勾股定理的应用,利用相似三角形的性质得到DF2=FOAF是解题答问题(2)的关键,依据相似三角形的性质求得GH的长是解答问题(3)的关键.△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系;(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FG∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD﹣GH求解即可.
GF,接下来,证明本题主要考查的是四边形与三角形的综合应用,解答本题主要应用了矩形的性质、菱形的判定和性质、相似三角形的性质和判定、勾股定理的应用,利用相似三角形的性质得到DF2=FOAF是解题答问题(2)的关键,依据相似三角形的性质求得GH的长是解答问题(3)的关键.△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系;(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FG∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD﹣GH求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.
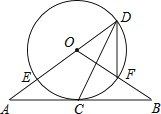
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的村料,再分解因式.
要把多项式
 分解因式,可以先把它的前两项分成组,并提出a,把它的后两项分成组,并提出b,从而得
分解因式,可以先把它的前两项分成组,并提出a,把它的后两项分成组,并提出b,从而得 .
.这时,由于
 中又有公困式
中又有公困式 ,于是可提公因式
,于是可提公因式 ,从而得到
,从而得到 ,因此有
,因此有


 .
.这种因式分解的方法叫做分组分解法,如果把一个多项式各个项分组并提出公因式后,它们的另一个因式正好相同,那么这个多项式就可以利用分组分解法来因式分解.
请用上面材料中提供的方法因式分解:

 请你完成分解因式下面的过程
请你完成分解因式下面的过程
 ______
______ ;
; .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:y=
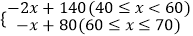 .
.
(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的位置如图所示,且|a|=|c|.
(1)若|a+c|+|b|=2,求b的值;
(2)用“>”从大到小把a,b,﹣b,c连接起来.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中
 直线
直线 与x轴、y轴相交于A、B两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转
与x轴、y轴相交于A、B两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转 得到CD,此时点D恰好落在直线AB上时,过点D作
得到CD,此时点D恰好落在直线AB上时,过点D作 轴于点E.
轴于点E. 求证:
求证: ≌
≌ ;
; 如图2,将
如图2,将 沿x轴正方向平移得
沿x轴正方向平移得 ,当直线
,当直线 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及 平移的距离;
平移的距离; 若点P在y轴上,点Q在直线AB上
若点P在y轴上,点Q在直线AB上 是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐;若不存在,请说明理由.
是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:
①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;
②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,
对于上述的两个判断,下列说法正确的是( )
A. ①正确,②错误 B. ①错误,②正确 C. ①,②都错误 D. ①,②都正确
相关试题

