【题目】如图所示,△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一锐角顶点B在y轴上.
(1)如图1所示,若AD于垂直x轴,垂足为点D.点C坐标是(-1,0),点A的坐标是(-3,1),求点B的坐标;
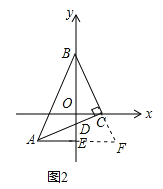
(2)如图2,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴于E,问BD与AE有怎样的数量关系,并说明理由;
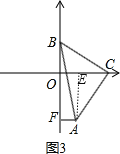
(3)如图3,直角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,两个结论①![]() 为定值;②
为定值;②![]() 为定值,只有一个结论成立,请你判断正确的结论加以证明,并求出这个定值.
为定值,只有一个结论成立,请你判断正确的结论加以证明,并求出这个定值.

参考答案:
【答案】(1)(0,2);(2)BD=2AE,理由见解析;(3)![]() =1,理由见解析
=1,理由见解析
【解析】
(1)只要求出Rt△ADC≌Rt△COB即可求;
(2)延长BC,AE交于点F,可证△ACF≌△BCD,可证△ABE≌△FBE,即可求得BD=2AE;
(3)作AE⊥OC,则AF=OE,可证△BCO≌△ACE,可得AF+OB=OC,即可解题.
解:∵点C坐标是(-1,0),点A的坐标是(-3,1),
∴AD=OC,
在Rt△ADC和Rt△COB中
![]() ,
,
∴Rt△ADC≌Rt△COB(HL),
∴OB=CD=2,
∴点B的坐标是(0,2);
(2)延长BC,AE交于点F,
∵AC=BC,AC⊥BC,
∴∠BAC=∠ABC=45°,
∵BD平分∠ABC,
∴∠CBD=22.5°,∠DAE=90°-∠ABD-∠BAD=22.5°,
在△ACF和△BCD中,
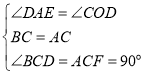 ,
,
∴△ACF≌△BCD(ASA),
∴AF=BD,
在△ABE和△FBE中,
 ,
,
∴△ABE≌△FBE(ASA),
∴AE=EF,
∴BD=2AE;
(3)作AE⊥OC,则AF=OE,
∵∠CBO+∠OBC=90°,∠OBC+∠ACO=90°,
∴∠ACO=∠CBO,
在△BCO和△ACE中,
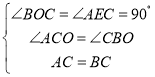 ,
,
∴△BCO≌△ACE(AAS),
∴CE=OB,
∴OB+AF=OC.
∴![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形
 中,
中, 、
、 分别是边
分别是边 、
、 的中点,
的中点, 分别交
分别交 、
、 于
于 、
、 .请判断下列结论:
.请判断下列结论: ;
; ;
; ;
; .其中正确的结论有( )
.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,
中, ,
, ,
, ,
, ,
, 是直线
是直线 ,
,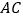 上的点.若由
上的点.若由 ,
, ,
, 构成的三角形与
构成的三角形与 相似,
相似, ,则
,则 的长为________.
的长为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 如果把一个三角形的各边扩大为原来的
 倍,那么它的周长也扩大为原来的
倍,那么它的周长也扩大为原来的 倍
倍B. 相似三角形对应高的比等于对应中线的比
C. 相似多边形的面积比等于周长比的平方
D. 如果把一个多边形的面积扩大为原来的
 倍,那么它的各边也扩大为原来的
倍,那么它的各边也扩大为原来的 倍
倍 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Δ
 中,∠
中,∠ =
= ,在同一平面内,现将Δ
,在同一平面内,现将Δ 围绕点
围绕点 旋转,使得点
旋转,使得点 落在点
落在点 ,点
,点 落在点
落在点 ,如果
,如果 ∥
∥ 那么∠
那么∠ =______
=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下五个方程:
①
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤
 其中一元二次方程有________(写序号)
其中一元二次方程有________(写序号) 请你选择其中的一个一元二次方程用适当的方法求出它的解.
请你选择其中的一个一元二次方程用适当的方法求出它的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Δ
 中,已知
中,已知 点
点 为
为 中点,点
中点,点 在线段
在线段 上以每秒
上以每秒 的速度由
的速度由 点向
点向 点运动,同时点
点运动,同时点 在线段
在线段 上由
上由 点向
点向 点运动。当点
点运动。当点 的运动速度为每秒____
的运动速度为每秒____ 时,能够在某一时刻使得Δ
时,能够在某一时刻使得Δ 与Δ
与Δ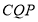 全等
全等
相关试题

