【题目】我们规定:横、纵坐标相等的点叫做“完美点”.
(1)若点A(x,y)是“完美点”,且满足x+y=4,求点A的坐标;
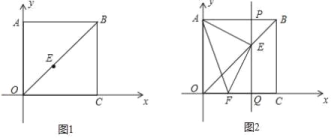
(2)如图1,在平面直角坐标系中,四边形OABC是正方形,点A坐标为(0,4),连接OB,E点从O向B运动,速度为2个单位/秒,到B点时运动停止,设运动时间为t.
①不管t为何值,E点总是“完美点”;
②如图2,连接AE,过E点作PQ⊥x轴分别交AB、OC于P、Q两点,过点E作EF⊥AE交x轴于点F,问:当E点运动时,四边形AFQP的面积是否发生变化?若不改变,求出面积的值;若改变,请说明理由.
参考答案:
【答案】(1)A(2,2);(2)①证明见解析;②当E点运动时,四边形AFQP的面积不变,面积为8.
【解析】
(1)根据“完美点”定义可求点A坐标;(2)①由题意可求直线OB的解析式y=x,点E在直线OB上移动,则可证结论;②根据题意可证△EFQ≌△APE,可求PE=FQ,则可求四边形AFQP的面积.
解(1)∵点A(x,y)是“完美点”
∴x=y
∵x+y=4
∴x=2,y=2
∴A点坐标(2,2)
(2)①∵四边形OABC是正方形,点A坐标为(0,4),
∴AO=AB=BC=4∴B(4,4)
设直线OB解析式y=kx过B点
∴4=4k,k=1
∴直线OB解析式y=x
设点E坐标(x,y)
∵点E在直线OB上移动
∴x=y
∴不管t为何值,E点总是“完美点”.
②∵E点总是“完美点”.
∴EQ=OQ
∵∠BAO=∠AOC=90°,PQ⊥x轴
∴四边形AOQP是矩形
∴AP=OQ,AO=PQ=4
∴AP=EQ
∵AE⊥EF
∴∠AEP+∠FEQ=90°,∠EAP+∠AEP=90°
∴∠FEQ=∠EAP
∵AP=EQ,∠FEQ=∠EAP,∠APE=∠EQF=90°
∴△APE≌△EFQ
∴PE=FQ
∵S四边形AFQP=![]() =2(PE+EQ)=2×PQ=8
=2(PE+EQ)=2×PQ=8
∴当E点运动时,四边形AFQP的面积不变,面积为8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC经过平移后得到△DEF,点A与点D,点B与点E,点C与点F分别是对应点,已知点A(3,3)、D(-2,1),解答下列问题:
(1)请在坐标系中画出平移后的△DEF;
(2)请直接写出以下点的坐标:B(___,___)、C(___,___)、E(___,___)、F(___,___);
(3)若点P(x,y)通过上述的平移规律平移得到的对应点为Q(3,5),则P点坐标为(____,____).

-
科目: 来源: 题型:
查看答案和解析>>【题目】小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明(包含设计费与印刷费),乙公司的收费与印刷卡片数量的关系如图2所示.
(1)分别写出甲乙两公司的收费y(元)与印刷数量x之间的关系式.
(2)如果你是小强,你会选择哪家公司?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x﹣15|+
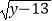 =0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=
=0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD= 
(1)求点B的坐标;
(2)求直线BN的解析式;
(3)将直线BN以每秒1个单位长度的速度沿y轴向下平移,求直线BN扫过矩形AOCB的面积S关于运动的时间t(0<t≤13)的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD是以BD为斜边的等腰直角三角形,△BCD中,∠DBC=90°,∠BCD=60°,DC中点为E,AD与BE的延长线交于点F,则∠AFB的度数为( )
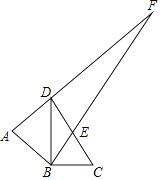
A.30°
B.15°
C.45°
D.25° -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.

(1)学校采用的调查方式是;学校共选取了名学生;
(2)补全统计图中的数据:条形统计图中羽毛球人、乒乓球人、其他人、扇形统计图中其他 %;
(3)该校共有1200名学生,请估计喜欢“乒乓球”的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M,N在半圆的直径AB上,点P,Q在
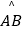 上,四边形MNPQ为正方形.若半圆的半径为
上,四边形MNPQ为正方形.若半圆的半径为 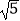 ,则正方形的边长为 .
,则正方形的边长为 . 
相关试题

