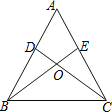
【题目】如图,点D、E分别为△ABC的边AB、AC上的点,BE与CD相交于点O,现有四个条件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD,选择其中2个条件作为题设,余下2个条件作为结论,所有命题中,真命题的个数为( )
A. .3B. .4C. .5D. 、6
参考答案:
【答案】C
【解析】
本题实际是考查全等三角形的判定,根据条件可看出主要是围绕三角形ABE和ACD全等来求解的.已经有了一个公共角∠A,只要再知道一组对应角和一组对应边相等即可得出三角形全等的结论.
解:第一种:命题的条件是①和③,命题的结论是②和④.
∵AB=AC,∠ABE=∠ACD,∠BAC=∠CAB,
∴△ABE≌△ACD.
∴BE=CD.
又∠BCD=∠ACB﹣∠ACD=∠ABC﹣∠ABE=∠CBE,
∴△BOC是等腰三角形.
∴OB=OC;
同理可得:第二种:命题的条件是②和③,命题的结论是①和④.
第三种:命题的条件是①和②,命题的结论是③和④.
第四种:命题的条件是③和④,命题的结论是②和①.
第五种:命题的条件是②和④,命题的结论是①和③.
故选:C.
-
科目: 来源: 题型:
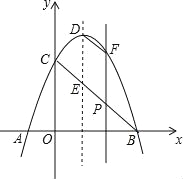
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,线段BC与抛物线的对称轴交于点E、P为线段BC上的一点(不与点B、C重合),过点P作PF∥y轴交抛物线于点F,连结DF.设点P的横坐标为m.
(1)求此抛物线所对应的函数表达式.
(2)求PF的长度,用含m的代数式表示.
(3)当四边形PEDF为平行四边形时,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,
 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示.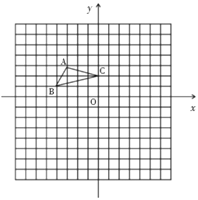
(1)直接写出
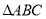 关于原点
关于原点 的中心对称图形
的中心对称图形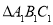 各顶点坐标:
各顶点坐标: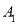 ________
________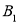 ________
________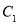 ________;
________;(2)将
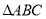 绕B点逆时针旋转
绕B点逆时针旋转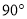 ,画出旋转后图形
,画出旋转后图形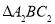 .求
.求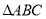 在旋转过程中所扫过的图形的面积和点
在旋转过程中所扫过的图形的面积和点 经过的路径长.
经过的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表,是池州市今年“五一”这周内日最高气温的统计表,关于这7天的日最高气温的众数,中位数,方差分别是:( )
日期
29日
30日
5月1日
2日
3日
4日
5日
日最高气温
16°C
19°C
22°C
24°C
26°C
24°C
23°C
A. 24,23,10B. 24,23,
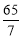 C. 24,22,10D. 24,22,
C. 24,22,10D. 24,22,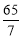
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是反比例函数y=
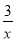 在第一象限内的图象上的两点,且A、B两点的横坐标分别是1和3,则S△AOB=_____.
在第一象限内的图象上的两点,且A、B两点的横坐标分别是1和3,则S△AOB=_____.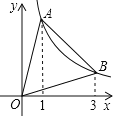
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠ABC=45°,AB=4
 ,BC=9,直线MN平分平行四边形ABCD的面积,分别交边AD、BC于点M、N,若△BMN是以MN为腰的等腰三角形,则BN=_____.
,BC=9,直线MN平分平行四边形ABCD的面积,分别交边AD、BC于点M、N,若△BMN是以MN为腰的等腰三角形,则BN=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,(k+1)2=k2+2k+1,变形得:(k+1)2﹣k2=2k+1,对上面的等式,依次令k=1,2,3,…得:
第1个等式:22﹣12=2×1+1
第2个等式:32﹣22=2×2+1
第3个等式:42﹣32=2×3+1
(1)按规律,写出第n个等式(用含n的等式表示):第n个等式 .
(2)记S1=1+2+3+…+n,将这n个等式两边分别相加,你能求出S1的公式吗?
相关试题

