【题目】在平面直角坐标系xOy中,直线AB:y=-x+b分别与x、y轴交于A(3,0)、B两点.

(1)如图,求点B的坐标;
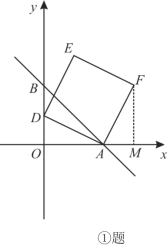
(2)点D为线段OB上的动点(点D不与点O重合),以AD为边,在第一象限内作正方形ADEF.
①如图,设点D为(0,m),请用含m的代数式表示点F的坐标;
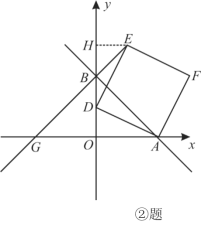
②如图,连结EB并延长交x轴于点G.当D点运动时,G点的位置是否发生变化?如果不变,请求出G点的坐标;如果变化,请说明理由.
参考答案:
【答案】(1)(0,3);(2)①F(m+3,3) ,②不变,(-3,0)
【解析】
(1)要求B点坐标,得先求函数表达式,然后代入求值即可.
(2)①根据题意作图,由正方形的性质证明出△DOA≌△AMF,用m表示各边长,即可表示出点F的坐标.
②过E作EH⊥x轴于H,由正方形的性质证明出△HDE≌△OAD,进而证出△BHE是等腰直角三角形,即证出△BOG为等腰直角三角形即得到结果.
解: (1)把A(3,0)坐标代入直线AB解析式y=-x+b,
得0=-3+b,
解得:b=3,
∴ 直线AB的解析式为y=-x+3,
当x=0时,y=3,
∴ 点B的坐标是(0,3);
(2)①过F作FM⊥x轴于M,则∠AMF=∠AOD=90°,
∵ 四边形ADEF正方形,
∴ AD=AF,∠DAF=90°,
∴ ∠DAO+∠FAM=90°,∠AFM+∠FAM=90°,
∴ ∠DAO=∠AFM,
∴ △DOA≌△AMF,
∴ FM=OA=3,AM=OD=m,
∴ OM=m+3,
∴ F(m+3,3) ;
② G点位置不变,坐标为:G(-3,0),
过E作EH⊥x轴于H则∠EHD=∠DOA=90°,
∵ 四边形ADEF正方形,
∴ AD=DE,∠ADE=90°,
∴ ∠ADO+∠HDE=90°,∠ADO+∠DAO=90°,
∴ ∠HDE=∠OAD,
∴ △HDE≌△OAD
∴ HE=OD,OA=DH,
∵ OA=OB,
∴ DH=OB,
∴ DH-BD=BO-BD,
即:BH=OD,
又HE=OD,
∴ BH=HE,
∴ △BHE是等腰直角三角形,
∴ ∠HBE=45°,
∴ ∠OBG=45°,
∴ △BOG为等腰直角三角形,
∴ OG=OB=3,
∴ G(-3,0).
方法二:同方法一先证△HDE≌△OAD ,
∴ HE=OD=m,OA=DH=3,
∴ E(m,m+3),
∵ B(0,3),
设直线BE的解析式为y=kx+b
则∵ m>0,
∴k=1,
∴ 直线BE的解析式为y=x+3,
当y=0时,x=-3,
∴ 点G的位置不变,坐标为(-3,0).
-
科目: 来源: 题型:
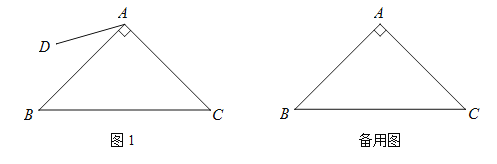
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)请根据题意补全图1;
(2)猜测BD和CE的数量关系并证明;
(3)作射线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,补全图形,直接写出PB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组从
 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位: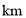 )
)第一次
第二次
第三次
第四次
第五次
第六次
第七次






(1)在第__________次记录时距
 地最远;
地最远;(2)求收工时距
 地多远?
地多远?(3)若每千米耗油
 升,每升汽油需
升,每升汽油需 元,问检修小组工作一天需汽油费多少元?
元,问检修小组工作一天需汽油费多少元? -
科目: 来源: 题型:
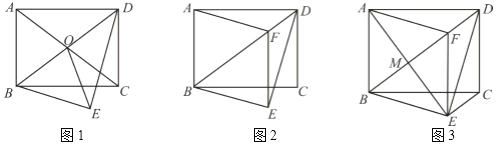
查看答案和解析>>【题目】在矩形ABCD中,AB=3,AD=4,将△ABD沿着BD折叠,使点A与点E重合.
(1)如图,对角线AC、BD相交于点O,连接OE,则线段OE的长= ;
(2)如图,过点E作EF∥CD交线段BD于点F,连接AF,求证:四边形ABEF是菱形;
(3)如图,在(2)条件下,线段AE、BD相交于M,连接CE,求线段CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 ,
, 分别在边
分别在边 ,
, 上,有下列条件:
上,有下列条件:①
 ;②
;② ;③
;③ ;④
;④ .其中,能使四边形
.其中,能使四边形 是平行四边形的条件有( ).
是平行四边形的条件有( ).
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=
 ;④S△AEF=
;④S△AEF= .其中正确的有( )
.其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将某点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这个点的“互换点”,如(-3,5)与(5,-3)是一对“互换点”.
(1)以O为圆心,半径为5的圆上有无数对“互换点”,请写出一对符合条件的“互换点”;
(2)点M,N是一对“互换点”,点M的坐标为(m,n),且(m>n),⊙P经过点M,N.
①点M的坐标为(4,0),求圆心P所在直线的表达式;
②⊙P的半径为5,求m-n的取值范围.
相关试题

