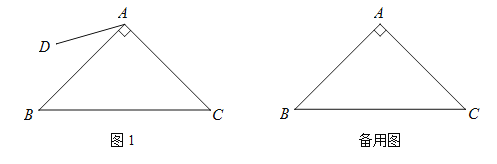
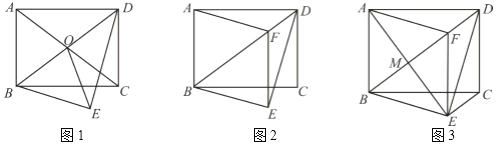
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)请根据题意补全图1;
(2)猜测BD和CE的数量关系并证明;
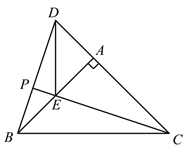
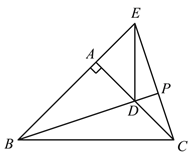
(3)作射线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,补全图形,直接写出PB的长.
参考答案:
【答案】(1)答案见解析;(2)BD=CE;(3)PB的长是![]() 或
或![]() .
.
【解析】试题分析:(1)根据题意画出图形即可;(2)根据“SAS”证明△ABD≌△ACE,从而可得BD=CE;(3)①根据“SAS”可证△ABD≌△ACE,从而得到∠ABD=∠ACE,再由两角对应相等的两个三角形相似可证△ACD∽△PBE,列比例方程可求出PB的长;②与①类似,先求出PD的长,再把PD和BD相加.
解:(1)如图
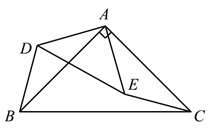
(2)BD和CE的数量是:BD=CE ;
∵∠DAB+∠BAE=∠CAE+∠BAE=90°,∴∠DAB=∠CAE.
∵AD=AE,AB=AC,∴△ABD≌△ACE,∴BD=CE.
(3)①CE=![]() .
.
∵△ABD≌△ACE, ∴∠ABD=∠ACE,
∴△ACD∽△PBE,
![]() ,
,
∴![]() ;
;
②∵△ABD∽△PDC,
![]() ,
,
∴![]() ;
;
∴PB=PD+BD=![]() .
.
∴PB的长是![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求作图.
(1)如图1,平行四边形ABCD,点E,F分别在边AD,BC上,且AE=CF,连接EF.请你只用无刻度直尺画出线段EF的中点O.(保留画图痕迹,不必说明理由).
(2)如图2,平行四边形ABCD,点E在边AB上,请你只用无刻度直尺在边CD上找一点F,使得四边形AECF为平行四边形,并说明理由.(注意:无刻度直尺只能过点画线段或直线或射线).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
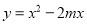 的顶点为点D.
的顶点为点D.(1)求点D的坐标(用含m的代数式表示);
(2)求函数
 的图象与x轴的交点坐标;
的图象与x轴的交点坐标;(3)若函数
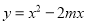 的图象在直线y=m的上方,求m的取值范围.
的图象在直线y=m的上方,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组从
 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位: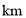 )
)第一次
第二次
第三次
第四次
第五次
第六次
第七次



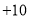



(1)在第__________次记录时距
 地最远;
地最远;(2)求收工时距
 地多远?
地多远?(3)若每千米耗油
 升,每升汽油需
升,每升汽油需 元,问检修小组工作一天需汽油费多少元?
元,问检修小组工作一天需汽油费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=3,AD=4,将△ABD沿着BD折叠,使点A与点E重合.
(1)如图,对角线AC、BD相交于点O,连接OE,则线段OE的长= ;
(2)如图,过点E作EF∥CD交线段BD于点F,连接AF,求证:四边形ABEF是菱形;
(3)如图,在(2)条件下,线段AE、BD相交于M,连接CE,求线段CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线AB:y=-x+b分别与x、y轴交于A(3,0)、B两点.

(1)如图,求点B的坐标;
(2)点D为线段OB上的动点(点D不与点O重合),以AD为边,在第一象限内作正方形ADEF.
①如图,设点D为(0,m),请用含m的代数式表示点F的坐标;
②如图,连结EB并延长交x轴于点G.当D点运动时,G点的位置是否发生变化?如果不变,请求出G点的坐标;如果变化,请说明理由.
相关试题

