Question

【题目】已知直线l：y=kx（k＜0），将直线y=kx沿y轴向下平移m（m＞0）个单位得到直线y=kx﹣m，平移后的直线与抛物线y=ax2相交于A（x1 ， y1），B（x2 ， y2）两点，抛物线y=ax2经过点P（6，﹣9）．
（1）求a的值；
（2）如图1，当∠AOB＜90°时，求m的取值范围；

（3）如图2，将抛物线y=ax2向右平移一个单位，再向上平移n个单位（n＞0）．若第一象限的抛物线上存在点M，N两点，且M，N两点关于直线y=x轴对称，求n的取值范围．

Answer 1

【答案】
（1）

解：∵抛物线y=ax2经过点P（6，﹣9），

∴36a=﹣9，

解得a=﹣

（2）

解：将y=kx﹣m代入y=﹣ x2，得 x2+kx﹣m=0，

∵y=kx﹣m与抛物线y=﹣ x2相交于A（x1，y1），B（x2，y2）两点，

∴y1=﹣ x12，y2=﹣ x22，x1x2=﹣4m，

∴y1y2=（﹣ x12）（﹣ x22）= （﹣4m）2=m2．

当∠AOB=90°时，如图1，过点A作AM⊥x轴于点M，过点B作BN⊥x轴于点N．

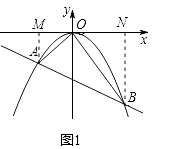
在△AOM与△OBN中，

，

∴△AOM∽△OBN，

∴ = ，即 = ，

∴y1y2=﹣x1x2，

∴m2=4m，

∵m＞0，

∴m=4，

∴当∠AOB＜90°时，m＞4

（3）

解：∵M，N两点关于直线y=x轴对称，

∴直线y=x是线段MN的垂直平分线，

∴直线MN的斜率为﹣1，OM=ON，

∴∠MOP=∠NOP，

∵∠GOP=∠HOP=45°，

∴∠GOM=∠HON．

如图2，设直线MN的解析式为y=﹣x+b，与平移后的抛物线y=﹣ （x﹣1）2+n交于M、N两点，交x轴于E点．分别过M，N作y轴、x轴垂线，垂足分别为G、H，

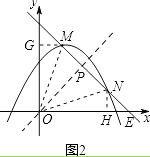
设M（m1，n1），N（m2，n2），直线MN与直线y=x交于点P．

在△OMG与△ONH中，

，

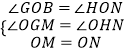∴△OMG≌△ONH，

∴MG=HN，即MG=HE．

将y=﹣ （x﹣1）2+n代入y=﹣x+b得： x2﹣ x+ +b﹣n=0，

由根与系数的关系得m1+m2=6，

∵OE=HE+OH=MG+OH=m1+m2=6，

∴b=6．

即 x2﹣ x+ ﹣n=0，

∵△＞0，

∴（﹣ ）2﹣4× ×（ ﹣n）＞0，

解得n＞4．

又M，N在第一象限，

∴m1m2=4（ ﹣n）＞0，

解得n＜ ，

∴n的取值范围是4＜n＜

【解析】（1）将点P（6，﹣9）的坐标代入y=ax2 ， 即可求出a的值；（2）将y=kx﹣m代入y=﹣ x2 ， 得 x2+kx﹣m=0，根据二次函数图象上点的坐标特征以及根与系数的关系得出y1=﹣ x12 ， y2=﹣ x22 ， x1x2=﹣4m，那么y1y2=m2 ． 当∠AOB=90°时，如图1，过点A作AM⊥x轴于点M，过点B作BN⊥x轴于点N．证明△AOM∽△OBN，根据相似三角形对应边成比例得出y1y2=﹣x1x2 ， 依此列出关于m的方程，求出m的值，进而得出当∠AOB＜90°时，m的取值范围；（3）根据轴对称的性质得出直线y=x是线段MN的垂直平分线，如图2，设直线MN的解析式为y=﹣x+b，与平移后的抛物线y=﹣ （x﹣1）2+n交于M、N两点，交x轴于E点，分别过M，N作y轴、x轴垂线，垂足分别为G、H，设M（m1 ， n1），N（m2 ， n2）．利用AAS证明△OMG≌△ONH，得出MG=HN，即MG=HE．将y=﹣ （x﹣1）2+n代入y=﹣x+b得： x2﹣ x+ +b﹣n=0，由根与系数的关系得m1+m2=6，则b=6，那么 x2﹣ x+ ﹣n=0，再根据△＞0以及M，N在第一象限分别列出不等式，进而求出n的取值范围．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．