Question

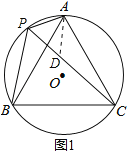
【题目】如图，A，P，B，C是⊙O上的四个点，∠APC=∠CPB=60°．

（1）判断△ABC的形状： ；

（2）试探究线段PA，PB，PC之间的数量关系，并证明你的结论．

Answer 1

【答案】（1）△ABC是等边三角形；（2）CP=BP+AP．

【解析】

试题分析：（1）利用圆周角定理可得∠BAC=∠CPB，∠ABC=∠APC，而∠APC=∠CPB=60°，所以∠BAC=∠ABC=60°，从而可判断△ABC的形状；

（2）在PC上截取PD=AP，则△APD是等边三角形，然后证明△APB≌△ADC，证明BP=CD，即可证得．

证明：（1）△ABC是等边三角形．

证明如下：在⊙O中，

∵∠BAC与∠CPB是对的圆周角，∠ABC与∠APC是所对的圆周角，

∴∠BAC=∠CPB，∠ABC=∠APC，

又∵∠APC=∠CPB=60°，

∴∠ABC=∠BAC=60°，

∴△ABC为等边三角形；

故答案为：△ABC是等边三角形；

（2）在PC上截取PD=AP，如图1，

又∵∠APC=60°，

∴△APD是等边三角形，

∴AD=AP=PD，∠ADP=60°，即∠ADC=120°．

又∵∠APB=∠APC+∠BPC=120°，

∴∠ADC=∠APB，

在△APB和△ADC中，

，

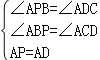∴△APB≌△ADC（AAS），

∴BP=CD，

又∵PD=AP，

∴CP=BP+AP．