Question

【题目】如图①，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG＝2OD，OE＝2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE.

(1)求证：DE⊥AG；

(2)正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角(0°＜α＜360°)得到正方形OE′F′G′，如图②.

①在旋转过程中，当∠OAG′是直角时，求α的度数；

②若正方形ABCD的边长为1，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．

Answer 1

【答案】（1）见解析 ；（2）①α＝30°或150° ，②α＝315°.

【解析】试题分析: （1）延长ED交AG于点H，易证△AOG≌△DOE，得到∠AGO=∠DEO，然后运用等量代换证明∠AHE=90°即可；

（2）①在旋转过程中，∠OAG′成为直角有两种情况：α由0°增大到90°过程中，当∠OAG′=90°时，α=30°，α由90°增大到180°过程中，当∠OAG′=90°时，α=150°；

②当旋转到A、O、F′在一条直线上时，AF′的长最大，AF′=AO+OF′=+2，此时α=315°．

试题解析:

(1)如图1,延长ED交AG于点H,

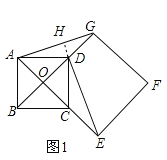
∵点O是正方形ABCD两对角线的交点，

∴OA=OD，OA⊥OD，

∵OG=OE，

在△AOG和△DOE中，

，

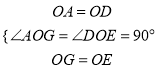∴△AOG≌△DOE，

∴∠AGO=∠DEO，

∵∠AGO+∠GAO=90°，

∴∠GAO+∠DEO=90°，

∴∠AHE=90°，

即DE⊥AG；

(2)①在旋转过程中,∠OAG′成为直角有两种情况：

(Ⅰ)α由0°增大到90°过程中,当∠OAG′=90°时，

∵OA=OD=OG=OG′，

∴在Rt△OAG′中,sin∠AG′O==，

∴∠AG′O=30°，

∵OA⊥OD,OA⊥AG′，

∴OD∥AG′,

∴∠DOG′=∠AG′O=30°，

即α=30°；

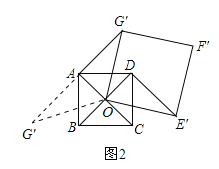
(Ⅱ)α由90°增大到180°过程中,当∠OAG′=90°时，

同理可求∠BOG′=30°，

∴α=180°30°=150°.

综上所述,当∠OAG′=90°时,α=30°或150°.

②如图3,当旋转到A.O、F′在一条直线上时,AF′的长最大，

∵正方形ABCD的边长为1，

∴OA=OD=OC=OB=，

∵OG=2OD，

∴OG′=OG=，

∴OF′=2，

∴AF′=AO+OF′=+2，

∵∠COE′=45°，

∴此时α=315°.

点睛: 本题考查的是正方形的性质、旋转变换的性质以及锐角三角函数的定义，掌握正方形的四条边相等、四个角相等，旋转变换的性质是解题的关键，注意特殊角的三角函数值的应用．