Question

【题目】线y＝a(x＋1)2的顶点为A，与y轴的负半轴交于点B，且OB＝OA.

(1)求抛物线的解析式；

(2)若点C(－3，m)在该抛物线上，求△ABC的面积．

Answer 1

【答案】(1) y＝－(x＋1)2；(2)3．

【解析】分析：（1）由抛物线解析式确定出顶点A坐标，根据OA=OB确定出B坐标，将B坐标代入解析式求出a的值，即可确定出解析式；（2）将C坐标代入抛物线解析式求出b的值，确定出C坐标，过C作CD垂直于x轴，三角形ABC面积=梯形OBCD面积-三角形ACD面积-三角形AOB面积，求出即可．

本题解析： (1)依题意可知A(－1，0)．由OB＝OA，得B(0，－1)．

将点B(0，－1)代入y＝a(x＋1)2，得－1＝a(0＋1)2，解得a＝－1.

所以y＝－(x＋1)2.

（2）过C作CD⊥x轴，

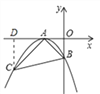
则S△ABC=S梯形OBCD-S△ACD-S△AOB=12×3×(4+1)-12×4×2-12×1×1=3．

(2)将C(－3，m)代入y＝－(x＋1)2，得m＝－(－3＋1)2，即m＝－4.所以C(－3，－4)．

所以S△ABC＝＝×1×4＋×1×3－×1×1＝3.