【题目】如果多项式x2+mx+16是另一个多项式的平方,那么m=_____.
参考答案:
【答案】±8.
【解析】
先根据两平方项确定出这两个数,再根据完全平方公式的乘积二倍项即可确定m的值.
∵x2+mx+16=x2+mx+42,
∴mx=±2×4×x,
解得m=±8.
故答案为:±8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣2mx﹣3(m≠0)与x轴交于A(3,0),B两点.
(1)求抛物线的表达式及点B的坐标;
(2)当﹣2<x<3时的函数图象记为G,求此时函数y的取值范围;
(3)在(2)的条件下,将图象G在x轴上方的部分沿x轴翻折,图象G的其余部分保持不变,得到一个新图象M.若经过点C(4.2)的直线y=kx+b(k≠0)与图象M在第三象限内有两个公共点,结合图象求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( )
A.矩形
B.菱形
C.对角线互相垂直的四边形
D.对角线相等的四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】平移后图形的位置是由_________________________________________所决定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD
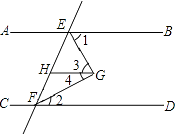
求证:∠EGF=90°
①把下列证明过程及理由补充完整.
②请你用精炼准确的文字将上述结论总结出来.
证明:∵HG∥AB(已知)
∴∠1=∠3 ()
又∵HG∥CD(已知)
∴∠2=∠4(同理)
∵AB∥CD(已知)
∴∠BEF+=180° ()
又∵EG平分∠BEF(已知)
∴∠1= ∠
∠
又∵FG平分∠EFD(已知)
∴∠2= ∠EFD (同理)
∠EFD (同理)
∴∠1+∠2= (+)
(+)
∴∠1+∠2=90°
∴∠3+∠4=90°
即∠EGF=90°. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,且∠ACB=( )时,则四边形AECF是正方形.

A.30°
B.45°
C.60°
D.90° -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市一月份的营业额为30万元,三月份的营业额为56万元.设每月的平均增长率为x,则可列方程为( )
A.56(1+x)2=30
B.56(1﹣x)2=30
C.30(1+x)2=56
D.30(1+x)3=56
相关试题

