【题目】如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,且∠ACB=( )时,则四边形AECF是正方形. 
A.30°
B.45°
C.60°
D.90°
参考答案:
【答案】D
【解析】解:过点E,F作EH⊥BD,FG⊥BD, ∵CE,CF为∠ACB,∠ACD的角平分线,
∴∠ECF=90°.
∵MN∥BC,
∴∠FEC=∠ECH,
∵∠ECH=∠ECO,
∴∠FEC=∠ECO,
∴OE=OC.
同理OC=OF,
∴OE=OF,
∵点O运动到AC的中点,
∴OA=OC,
∴四边形AECF为一矩形,
若∠ACB=90°,则CE=CF,
∴四边形AECF为正方形.
故选:D.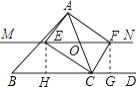
由题意可得四边形AECF为一矩形,要使四边形AECF是正方形,只需添加一条件,使其邻边相等即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平移后图形的位置是由_________________________________________所决定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果多项式x2+mx+16是另一个多项式的平方,那么m=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD
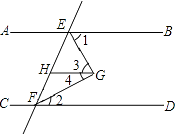
求证:∠EGF=90°
①把下列证明过程及理由补充完整.
②请你用精炼准确的文字将上述结论总结出来.
证明:∵HG∥AB(已知)
∴∠1=∠3 ()
又∵HG∥CD(已知)
∴∠2=∠4(同理)
∵AB∥CD(已知)
∴∠BEF+=180° ()
又∵EG平分∠BEF(已知)
∴∠1= ∠
∠
又∵FG平分∠EFD(已知)
∴∠2= ∠EFD (同理)
∠EFD (同理)
∴∠1+∠2= (+)
(+)
∴∠1+∠2=90°
∴∠3+∠4=90°
即∠EGF=90°. -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市一月份的营业额为30万元,三月份的营业额为56万元.设每月的平均增长率为x,则可列方程为( )
A.56(1+x)2=30
B.56(1﹣x)2=30
C.30(1+x)2=56
D.30(1+x)3=56 -
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式x2-8x+a可化为(x-b)2+1,则a+b=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解
(1)2x3﹣8x
(2)x2﹣2x﹣3
(3)4a2+4ab+b2﹣1
相关试题

