【题目】如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)若∠AOC=50°,求出∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.

参考答案:
【答案】(1)155°;(2)证明见解析.
【解析】试题分析:(1)已知OD平分∠AOC,根据角平分线的定义求得∠AOD的度数,再由平角的定义求得∠BOD的度数;(2)已知OD平分∠AOC,根据角平分线的定义求得∠AOD的度数,再求得∠COE和∠BOE的度数,即可判断OE是否平分∠BOC.
试题解析:
(1)∵OD平分∠AOC
∴∠AOD=![]() ∠AOC =
∠AOC = ![]()
∴∠BOD=![]() -∠AOD
-∠AOD
=![]() -
-![]()
=![]()
(2)∵OD平分∠AOC
∴∠COD=![]() ∠AOC=
∠AOC= ![]()
∴∠COE=![]() -∠COD=
-∠COD=![]()
∴∠BOE=![]() -∠AOC-∠COE=
-∠AOC-∠COE=![]() -
-![]() -
-![]() =
=![]()
∴∠COE=∠BOE,即OE平分∠BOC
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,不能判定两个直角三角形全等的是( )
A. 两个锐角对应相等 B. 一条直角边和一个锐角对应相等
C. 两条直角边对应相等 D. 一条直角边和一条斜边对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(y3)2+(y2)3=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列一元一次方程:
(1)
 (2)
(2)
(3)
 (4)
(4)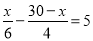
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边三角形绕着它的中心O旋转,若旋转后的三角形能与自身重合,则旋转角最小是( )
A.360°B.240°C.120°D.60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,M是边AB的中点,D是边BC延长线上的一点,且CD=
 BC,作DN∥CM交AC于点N.求证:四边形MCDN是平行四边形.
BC,作DN∥CM交AC于点N.求证:四边形MCDN是平行四边形. 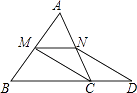
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和加上它的外角和等于1260°,求此多边形的边数。
相关试题

