【题目】如图,在四边形ABCD中,∠B=90°,过点D作DE∥AB,交BC于E,且DE=BC,连接AC交AC于F,若∠ACB=∠CDE=30°,则图中有几个等腰三角形?请找出来并说明理由. 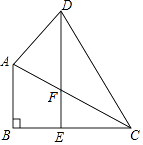
参考答案:
【答案】解:共有两个等腰三角形,分别是△ACD,△DCF.
理由:∵DE∥AB,
∴∠DEC=∠B,
在△DCE和△CAB中,
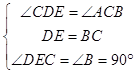 ,
,
∴△DCE≌△CAB,
∴CA=CD,
∴△ACD是等腰三角形,
∵∠B=90°,
∴∠DEC=90°,
∵∠ACB=∠CDE=30°,
∴∠DCE=90°﹣∠CDE=60°,
∴∠DCF=∠DCE﹣∠ACE=30°=∠CDE,
∴DF=CF,
∴△DCF是等腰三角形.
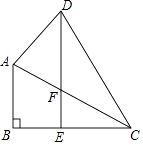
【解析】首先证明△DCE≌△CAB推出CA=CD,再证明∠FCD=∠FDC=30°即可解决问题.
【考点精析】本题主要考查了平行线的性质和等腰三角形的判定的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与点A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F、D.
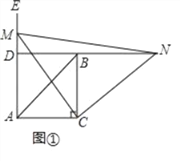

(1)问题发现:直接写出∠NDE= 度;
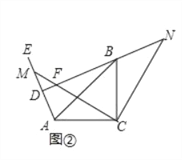
(2)拓展探究:试判断,如图②当∠EAC为钝角时,其他条件不变,∠NDE的大小有无变化?请给出证明.
(3)如图③,若∠EAC=15°,BD=
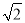 ,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.
,直线CM与AB交于点G,其他条件不变,请直接写出AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x的顶点为( )
A.(1,1)
B.(2,﹣4)
C.(﹣1,1)
D.(1,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段a=3,c=12,则线段a和c的比例中项b是( )
A.±6B.36C.6D.﹣6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个相似三角形对应的高之比是2:3,那么它们对应的角平分线之比是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,属于必然事件的是()
A.男生一定比女生高
B.掷一枚均匀的骰子,落地后偶数点朝上
C.在操场上抛出的篮球会下落
D.天气一天比一天冷 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+1的最小值是 .
相关试题

