【题目】如图1,抛物线![]() :
:![]() 与
与![]() :
:![]() 相交于点O、C,
相交于点O、C,![]() 与
与![]() 分别交x轴于点B、A,且B为线段AO的中点.
分别交x轴于点B、A,且B为线段AO的中点.
(1)求![]() 的值;
的值;
(2)若OC⊥AC,求△OAC的面积;
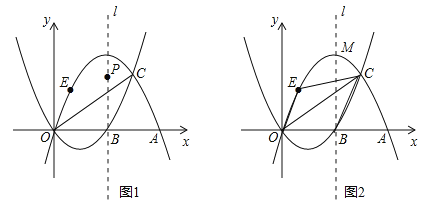
(3)抛物线C2的对称轴为l,顶点为M,在(2)的条件下:
①点P为抛物线C2对称轴l上一动点,当△PAC的周长最小时,求点P的坐标;
②如图2,点E在抛物线C2上点O与点M之间运动,四边形OBCE的面积是否存在最大值?若存在,求出面积的最大值和点E的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①P(
;(3)①P(![]() ,
,![]() );②E(
);②E(![]() ,
,![]() ),
),![]() .
.
【解析】
试题分析:(1)由两抛物线解析式可分别用a和b表示出A、B两点的坐标,利用B为OA的中点可得到a和b之间的关系式;
(2)由抛物线解析式可先求得C点坐标,过C作CD⊥x轴于点D,可证得△OCD∽△CAD,由相似三角形的性质可得到关于a的方程,可求得OA和CD的长,可求得△OAC的面积;
(3)①连接OC与l的交点即为满足条件的点P,可求得OC的解析式,则可求得P点坐标;
②设出E点坐标,则可表示出△EOB的面积,过点E作x轴的平行线交直线BC于点N,可先求得BC的解析式,则可表示出EN的长,进一步可表示出△EBC的面积,则可表示出四边形OBCE的面积,利用二次函数的性质可求得其最大值,及E点的坐标.
试题解析:
(1)在y=x2+ax中,当y=0时,x2+ax=0,x1=0,x2=﹣a,∴B(﹣a,0),在y=﹣x2+bx中,当y=0时,﹣x2+bx=0,x1=0,x2=b,∴A(0,b),∵B为OA的中点,∴b=﹣2a,∴![]() ;
;
(2)联立两抛物线解析式可得: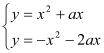 ,消去y整理可得
,消去y整理可得![]() ,解得
,解得![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,∴C(
,∴C(![]() ,
,![]() ),过C作CD⊥x轴于点D,如图1,∴D(
),过C作CD⊥x轴于点D,如图1,∴D(![]() ,0),∵∠OCA=90°,∴△OCD∽△CAD,∴
,0),∵∠OCA=90°,∴△OCD∽△CAD,∴![]() ,∴CD2=ADOD,即
,∴CD2=ADOD,即![]() ,∴a1=0(舍去),
,∴a1=0(舍去),![]() (舍去),
(舍去),![]() ,∴OA=-2a=
,∴OA=-2a=![]() ,CD=
,CD=![]() =1,∴
=1,∴![]() ;
;
(3)①抛物线![]() ,∴其对称轴
,∴其对称轴![]() ,点A关于l2的对称点为O(0,0),C(
,点A关于l2的对称点为O(0,0),C(![]() ,1),则P为直线OC与l2的交点,设OC的解析式为y=kx,∴1=
,1),则P为直线OC与l2的交点,设OC的解析式为y=kx,∴1=![]() k,得k=
k,得k=![]() ,∴OC的解析式为
,∴OC的解析式为![]() ,当
,当![]() 时,
时,![]() ,∴P(
,∴P(![]() ,
,![]() );
);
②设E(m,![]() )(
)(![]() ),则
),则![]() ,而B(
,而B(![]() ,0),C(
,0),C(![]() ,1),设直线BC的解析式为y=kx+b,由
,1),设直线BC的解析式为y=kx+b,由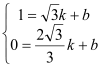 ,解得:k=
,解得:k=![]() ,b=-2,∴直线BC的解析式为
,b=-2,∴直线BC的解析式为![]() ,过点E作x轴的平行线交直线BC于点N,如图2,则
,过点E作x轴的平行线交直线BC于点N,如图2,则![]() ,即x=
,即x=![]()
∴EN=![]()
∴![]()
∴S四边形OBCE=S△OBE+S△EBC![]()
![]() ,∵
,∵![]() ,∴当
,∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,∴E(
,∴E(![]() ,
,![]() ),
),![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):
 .
.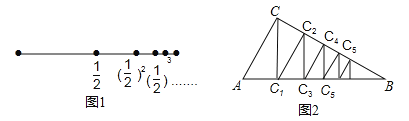
图2也是一种无限分割:在△ABC中,∠C=90°,∠B=30°,过点C作CC1⊥AB于点C1,再过点C1作C1C2⊥BC于点C2,又过点C2作C2C3⊥AB于点C3,如此无限继续下去,则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn﹣2Cn﹣1Cn、….假设AC=2,这些三角形的面积和可以得到一个等式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)999×1001
(2)2015+20152﹣2015×2016
(3)[a2+b2+2b(a﹣b)﹣(a﹣b)2]÷4b. -
科目: 来源: 题型:
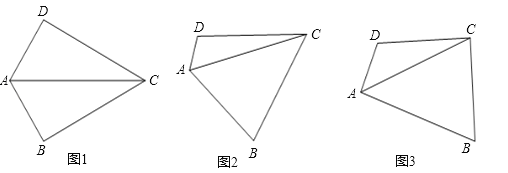
查看答案和解析>>【题目】在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD.
(1)如图1,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC的数量关系并说明理由.
(2)如图2,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下各组数分别是三条线段的长度,其中可以构成三角形的是( )
A. 1,3,4 B. 1,2,3 C. 6,6,10 D. 1,4,6
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:

(1)在表中:m= ,n= ;
(2)补全频数分布直方图;
(3)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在 组;
(4)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
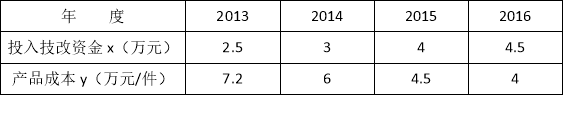
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
相关试题

