【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
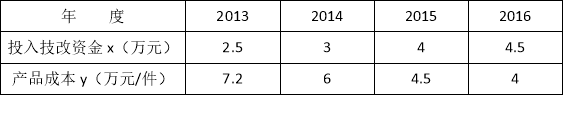
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
参考答案:
【答案】(1)![]() ;(2)①0.4;②1.13.
;(2)①0.4;②1.13.
【解析】
试题分析:(1)根据实际题意和数据特点分情况求解,根据排除法可知其为反比例函数,利用待定系数法求解即可;
(2)①直接把x=5万元代入函数解析式即可求解;
②直接把y=3.2万元代入函数解析式即可求解;
试题解析:(1)设其为一次函数,解析式为y=kx+b,当x=2.5时,y=7.2;当x=3时,y=6,∴![]() ,解得k=﹣2.4,b=13.2,∴一次函数解析式为y=﹣2.4x+13.2.
,解得k=﹣2.4,b=13.2,∴一次函数解析式为y=﹣2.4x+13.2.
把x=4时,y=4.5代入此函数解析式,左边≠右边,∴其不是一次函数.
同理.其也不是二次函数.
设其为反比例函数.解析式为![]() .
.
当x=2.5时,y=7.2,可得:7.2=![]() ,解得k=18
,解得k=18
∴反比例函数是![]() .
.
验证:当x=3时,y=![]() =6,符合反比例函数.
=6,符合反比例函数.
同理可验证x=4时,y=4.5,x=4.5时,y=4成立.
可用反比例函数![]() 表示其变化规律.
表示其变化规律.
(2)①当x=5万元时,y=3.6.
4﹣3.6=0.4(万元),∴生产成本每件比2009年降低0.4万元.
②当y=3.2万元时,3.2=![]() ,∴x=5.625,∴5.625﹣4.5=1.125≈1.13(万元)
,∴x=5.625,∴5.625﹣4.5=1.125≈1.13(万元)
∴还约需投入1.13万元.
-
科目: 来源: 题型:
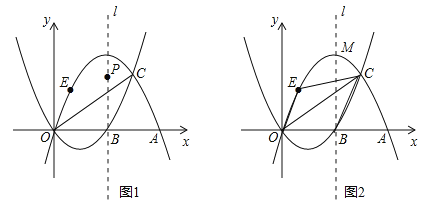
查看答案和解析>>【题目】如图1,抛物线
 :
: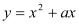 与
与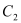 :
: 相交于点O、C,
相交于点O、C, 与
与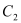 分别交x轴于点B、A,且B为线段AO的中点.
分别交x轴于点B、A,且B为线段AO的中点.(1)求
 的值;
的值;(2)若OC⊥AC,求△OAC的面积;
(3)抛物线C2的对称轴为l,顶点为M,在(2)的条件下:
①点P为抛物线C2对称轴l上一动点,当△PAC的周长最小时,求点P的坐标;
②如图2,点E在抛物线C2上点O与点M之间运动,四边形OBCE的面积是否存在最大值?若存在,求出面积的最大值和点E的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下各组数分别是三条线段的长度,其中可以构成三角形的是( )
A. 1,3,4 B. 1,2,3 C. 6,6,10 D. 1,4,6
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:

(1)在表中:m= ,n= ;
(2)补全频数分布直方图;
(3)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在 组;
(4)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.

-
科目: 来源: 题型:
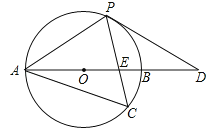
查看答案和解析>>【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=4,求CECP的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-1,0)、B(4,0)、C(0,2)三点.
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1-S2的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,若AE=13,求AF的长度.

相关试题

