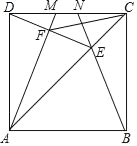
【题目】如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为4,则线段CF的最小值是_____.
参考答案:
【答案】2![]() ﹣2
﹣2
【解析】分析:根据正方形的性质可得AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,然后利用“HL”证明Rt△ADM和Rt△BCN全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△DCE和△BCE全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AFD=90°,取AD的中点O,连接OF、OC,根据直角三角形斜边上的中线等于斜边的一半可得OF=![]() AD=2,利用勾股定理列式求出OC,然后根据三角形的三边关系可知当O、F、C三点共线时,CF的长度最小.
AD=2,利用勾股定理列式求出OC,然后根据三角形的三边关系可知当O、F、C三点共线时,CF的长度最小.
详解:在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE.在Rt△ADM和Rt△BCN中,![]() ,∴Rt△ADM≌Rt△BCN(HL),∴∠1=∠2.在△DCE和△BCE中,
,∴Rt△ADM≌Rt△BCN(HL),∴∠1=∠2.在△DCE和△BCE中,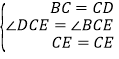 ,∴△DCE≌△BCE(SAS),∴∠2=∠3,∴∠1=∠3.
,∴△DCE≌△BCE(SAS),∴∠2=∠3,∴∠1=∠3.
∵∠ADF+∠3=∠ADC=90°,∴∠1+∠ADF=90°,∴∠AFD=180°﹣90°=90°,取AD的中点O,连接OF、OC,则OF=DO=![]() AD=2.在Rt△ODC中,OC=
AD=2.在Rt△ODC中,OC=![]() =
=![]() =2
=2![]() ,根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=2
,根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=2![]() ﹣2.
﹣2.
故答案为:2![]() ﹣2.
﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在等边三角形ABC中,点E在线段AB上,点D在CB的延长线上,
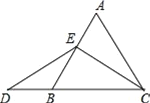
(1)试证明△DEC是等腰三角形;(2)在图中找出与AE相等的线段,并证明
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连结AF、BD.
(1)观察图形,猜想AF与BD之间有怎样的关系,并证明你的猜想;
(2)若将正方形CDEF绕点C按顺时针方向旋转,使正方形CDEF的一边落在△ABC的内部,请你画出一个变换后的图形,并对照已知图形标记字母,题(1)中猜想的结论是否仍然成立?若成立,直接写出结论,不必证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC=2,∠A=∠B=30°,点D在线段AB上运动(点D不与A、B重合),连接CD,作∠CDE=30°,DE交BC于点E.
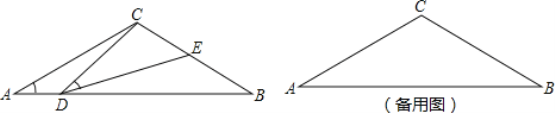
(1)AB=;
(2)当AD等于多少时,△ADC≌△BED,请说明理由;
(3)在点D的运动过程中,△CDE的形状可以是等腰三角形吗?若可以,求出AD的长;若不可以,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.

小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).
参考小炎同学思考问题的方法,解决下列问题:
(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足_ 关系时,仍有EF=BE+DF;
(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE的长.
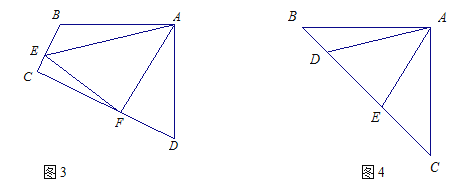
-
科目: 来源: 题型:
查看答案和解析>>【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期
一
二
三
四
五
六
日
增减
-5
+7
-3
+4
+10
-9
-25
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)

(2)
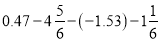
(3)
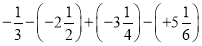
(4)
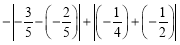
(5)
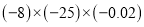
(6)
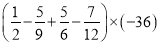
相关试题

