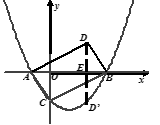
【题目】如图,抛物线y=x2-x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=-2x上.
【1】求a的值;
【2】求A,B的坐标;
【3】以AC,CB为一组邻边作□ACBD,则点D关于x轴的对称点D′ 是否在该抛物线上?请说明理由.

参考答案:
【答案】
【1】抛物线的顶点坐标为(1,a-)
∵顶点在直线y=-2x上,∴a-=-2.即a=-
【2】由(1)知,抛物线表达式为y=x2-x- ,
令y=0,得x2-x- =0.解之得:x1=-1,x3=3.
∴A的坐标 (-1,0),B的坐标 (3,0);
【3】∵四边形ABCD是平行四边形,
∴点C,D关于对角线交点(1,0)对称又∵点D′ 是点D关于x轴的对称点,点C,D′ 关于抛物线的对称轴对称.∴D′ 在抛物线上.
【解析】(1)根据抛物线的顶点在直线y=-2x上,运用待定系数法求得
(2)由(1)得抛物线的解析式,因为A,B的坐标在x轴上,所以纵坐标为0,代入抛物线的解析式,解一元二次方程可求得A,B的坐标
(3)由平行四边形知C,D关于对角线交点对称,通过点D′ 是点D关于x轴的对称点,可知点C,D′ 关于抛物线的对称轴对称,即可得出结论
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别
成本价(元/箱)
销售价(元/箱)
甲
25
35
乙
35
48
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形OABC的边长为2,顶点A,C分别在x轴,y轴的正半轴上,点E是BC的中点,F是AB延长线上一点且FB=1.

(1)求经过点O,A,E三点的抛物线解析式;
(2)点P在抛物线上运动,当点P运动到什么位置时△OAP的面积为2,请求出点P的坐标;
(3)在抛物线上是否存在一点Q,使△AFQ是等腰直角三角形?若存在直接写出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 经过
经过 顶点
顶点 的一条直线,
的一条直线, .
. 分别是直线
分别是直线 上两点,且
上两点,且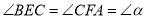 .
.(1)若直线
 经过
经过 的内部,且
的内部,且 在射线
在射线 上,请解决下面两个问题:
上,请解决下面两个问题:①如图1,若
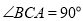 ,
, ,
,则
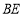
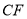 ;
;
 (填“
(填“ ”,“
”,“ ”或“
”或“ ”);
”);②如图2,若
 ,请添加一个关于
,请添加一个关于 与
与 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线
 经过
经过 的外部,
的外部, ,请提出
,请提出 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,若二次函数
 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数 的图象的对称点为C。
的图象的对称点为C。(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数
 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解本校七年级学生数学学习情况,随机抽查该年级若干名学生进行测试,然后把测试结果分为
 个等级:
个等级: ,并将统计结果绘制成两幅不完整的统计图,请根据图中的信息解答下列问题:
,并将统计结果绘制成两幅不完整的统计图,请根据图中的信息解答下列问题:
 补全条形统计图;
补全条形统计图; 等级为
等级为 等的所在扇形的圆心角是 度;
等的所在扇形的圆心角是 度; 如果七年级共有学生
如果七年级共有学生 名,请估算该年级学生中数学学习为
名,请估算该年级学生中数学学习为 等和
等和 等的共多少人?
等的共多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.

相关试题

