【题目】某校为了解本校七年级学生数学学习情况,随机抽查该年级若干名学生进行测试,然后把测试结果分为![]() 个等级:
个等级:![]() ,并将统计结果绘制成两幅不完整的统计图,请根据图中的信息解答下列问题:
,并将统计结果绘制成两幅不完整的统计图,请根据图中的信息解答下列问题:

![]() 补全条形统计图;
补全条形统计图;
![]() 等级为
等级为![]() 等的所在扇形的圆心角是 度;
等的所在扇形的圆心角是 度;
![]() 如果七年级共有学生
如果七年级共有学生![]() 名,请估算该年级学生中数学学习为
名,请估算该年级学生中数学学习为![]() 等和
等和![]() 等的共多少人?
等的共多少人?
参考答案:
【答案】![]() 见解析
见解析![]()
![]()
![]() 约有
约有![]() 人.
人.
【解析】
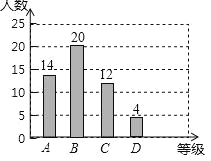
(1)从统计图中可以得到A等级的有14人,占调查人数的28%,可求出调查人数,B等级占40%,可求出B等级人数,即可补全条形统计图,
(2)用360°乘以C等级所占的百分比,即可求出度数,
(3)样本估计总体,样本中A等级、B等级共占(28%+40%)总人数为50人,即可求出A、B两个等级的人数.
解:(1)调查总人数为:14÷28%=50人,B等级的人数为:50×40%=20人,补全条形统计图如图所示:
(2)360°×![]() =86.4°.
=86.4°.
故答案为:86.4.
(3)900×(28%+40%)=612人,
答:该年级我校学生中数学学习A等和B等的约有612人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 经过
经过 顶点
顶点 的一条直线,
的一条直线, .
. 分别是直线
分别是直线 上两点,且
上两点,且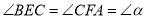 .
.(1)若直线
 经过
经过 的内部,且
的内部,且 在射线
在射线 上,请解决下面两个问题:
上,请解决下面两个问题:①如图1,若
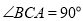 ,
, ,
,则
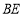
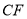 ;
;
 (填“
(填“ ”,“
”,“ ”或“
”或“ ”);
”);②如图2,若
 ,请添加一个关于
,请添加一个关于 与
与 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线
 经过
经过 的外部,
的外部, ,请提出
,请提出 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2-x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=-2x上.
【1】求a的值;
【2】求A,B的坐标;
【3】以AC,CB为一组邻边作□ACBD,则点D关于x轴的对称点D′ 是否在该抛物线上?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,若二次函数
 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数 的图象的对称点为C。
的图象的对称点为C。(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数
 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,﹣2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】《代数学》中记载,形如x2+10x=39的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为
 x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( )
x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( ) 
A.6B.3
 -3C.3
-3C.3 -2D.3
-2D.3 -
-
相关试题

