【题目】如图,在直角△ABC中,∠BAC=90°,AB=3,M是边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好在边AC的中点处,那么点M到AC的距离是( )

A. 1.5 B. 2 C. 2.5 D. 3
参考答案:
【答案】B
【解析】
作ME⊥AC,证明△CEM∽△CAB,然后利用折叠的性质和相似三角形的性质列出方程解答.
解:如图,作ME⊥AC于E,则∠MEC=90°,
又∵在Rt△ABC中,∠BAC=90°,
∴∠MEC=∠BAC,
∴ME∥AB,
∴∠BAM=∠EMA=45°(两直线平行,内错角相等),
∵∠BAM=∠MAC=45°,
∴∠MAE=∠AME=45°,
∴ME=AE,
∵ME∥AB,
∴△CEM∽△CAB,
∴![]() ,
,
解得:ME=2,
所以点M到AC的距离是2.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级某班为准备科技节表彰的奖品,计划从友谊超市购买笔记本和水笔共40件,在获知某网店有“五一”促销活动后,决定从该网店购买这些奖品.已知笔记本和水笔在这两家商店的零售价分别如下表,且在友谊超市购买这些奖品需花费90元.
品名商店
笔记本(元/件)
水笔(元/件)
友谊超市
2.4
2
网店
2
1.8
(1)请求出需购买笔记本和水笔的数量;
(2)求从网店购买这些奖品可节省多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级全体同学参加了“爱心一日捐捐款活动,该校随杋抽査了部分同学捐款的情况统计如图所示:

(1)求出本次抽查的学生人数;
(2)求出捐款10元的学生人数,并将条形图补充完整;
(3)捐款金额的众数是 元,中位数是 .
(4)请估计全校八年级1000名学生,捐款20元的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2).

(1)求直线AB的函数表达式;
(2)若在y轴上存在一点M,使MA+MB的值最小,请求出点M的坐标;
(3)在x轴上是否存在点N,使△AON是等腰三角形?如果存在,直接写出点N的坐标;如果不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠A=36°,∠C=72°,∠ABC的平分线交AC于D,则图中共有等腰三角形( )
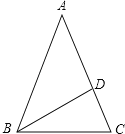
A.0个B.1个C.2个D.3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,证明:AB=FA+BD;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.

相关试题

