【题目】如图,已知∠ADC=∠EFC,∠3=∠C,证明∠1=∠2的过程如下,请填上对应的理由.
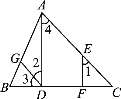
解:∵∠ADC=∠EFC(已知),
∴AD∥EF(___________________________________).
∴∠1=∠4(__________________________________).
又∵∠3=∠C(已知),
∴AC∥DG(__________________________________).
∴∠2=∠4(_________________________________).
∴∠1=∠2(________________________).
参考答案:
【答案】同位角相等,两直线平行;两直线平行,同位角相等;同位角相等,两直线平行;两直线平行,内错角相等;等量代换.
【解析】
由∠ADC=∠EFC,根据同位角相等,两直线平行,可判定AD∥EF,继而可得∠1=∠4,又由∠3=∠C,易判定AC∥DG,继而可得∠2=∠4,利用等量代换即可得∠1=∠2.
∵∠ADC=∠EFC(已知),
∴AD∥EF(同位角相等,两直线平行).
∴∠1=∠4(两直线平行,同位角相等).
又∵∠3=∠C(已知),
∴AC∥DG(同位角相等,两直线平行).
∴∠2=∠4(两直线平行,内错角相等).
∴∠1=∠2(等量代换),
故答案为:同位角相等,两直线平行;两直线平行,同位角相等;同位角相等,两直线平行;两直线平行,内错角相等;等量代换.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD沿EF折叠后,ED交BC于点G,点D、C分别落在点D′、C′位置上,若∠EFG=55°,∠BGE=_____度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O,A,B,C的坐标分别为(0,0),(-1,2),(-3,3)和(-2,1).
(1)若图中的各个点的纵坐标不变,横坐标都乘-1,与原图案相比,所得图案有什么变化?画出图形并说明一下变化.
(2)若图中的各个点的横坐标不变,纵坐标都乘-1,与原图案相比,所得图案有什么变化?画出图形并说明一下变化.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产某种产品,每件产品的生产成本为25元,出厂价为50元.在生产过程中,平均每生产一件这种产品有0.5m3的污水排出.为净化环境,该厂购买了一套污水处理设备,每处理1m3污水所需原材料费为2元,每月排污设备耗费4000元.
(1)请给出该厂每月的利润与产品件数的函数关系式;
(2)为保证每月盈利30000元,该厂每月至少需生产并销售这种产品多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知它们的总辆数为 16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出哪种方案的运费最省?最省是多少元?
-
科目: 来源: 题型:
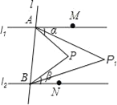
查看答案和解析>>【题目】如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
(1)当点P在l1与l2之间时.
①求∠APB的大小(用含α、β的代数式表示);
②若∠PAM的平分线与∠PBN的平分线交于点P1,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,则∠AP1B= ,∠APnB= .(用含α、β的代数式表示,其中n为正整数)
(2)当点P不在l1与l2之间时.
若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=
 ,反比例函数y=
,反比例函数y= 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式
(2)若函数y=3x与y= 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比
相关试题

