【题目】如图,抛物线 ![]() 与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,
与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,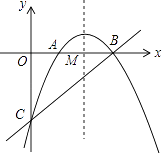
(1)求△ABC的面积;
(2)若p是x轴上方的抛物线上的一个动点,求点P到直线BC的距离的最大值;
(3)若点P在抛物线上运动(点P异于点A),当∠PCB=∠BCA时,求直线PC的解析式.
参考答案:
【答案】
(1)
解:令y=0,则有﹣ ![]() x2+4x﹣6=﹣
x2+4x﹣6=﹣ ![]() (x﹣2)(x﹣6)=0,
(x﹣2)(x﹣6)=0,
解得:x1=2,x2=6,
即点A(2,0),点B(6,0).
令x=0,则y=﹣6,
即点C(0,6).
∴AB=4,CO=6.
△ABC的面积S△ABC= ![]() ABCO=
ABCO= ![]() ×4×6=12
×4×6=12
(2)
解:设直线BC的解析式为y=kx+b,
∵点B(6,0),点C(0,﹣6),
∴有 ![]() ,解得
,解得 ![]() ,
,
∴直线BC的解析式为y=x﹣6.
设经过动点P且平行于直线BC的直线解析式为y1=x+a.
将y1=x+a代入抛物线y=﹣ ![]() x2+4x﹣6中得:
x2+4x﹣6中得: ![]() x2﹣3x+6+a=0,
x2﹣3x+6+a=0,
若直线y1=x+a与抛物线相切,则有:
△=(﹣3)2﹣4× ![]() ×(6+a)=0,即3+2a=0,
×(6+a)=0,即3+2a=0,
解得:a=﹣ ![]() .
.
∴ ![]() ﹣3x+6﹣
﹣3x+6﹣ ![]() =0,即x2﹣6x+9=0,
=0,即x2﹣6x+9=0,
解得:x=3,
将x=3代入y1=x﹣ ![]() ,得y1=
,得y1= ![]() ,
,
∴此时P点坐标为(3, ![]() )在x轴上方.
)在x轴上方.
∵直线BC的解析式为x﹣y﹣6=0,
∴点P到直线BC的距离= ![]() =
= ![]() .
.
故点P到直线BC的距离的最大值为 ![]()
(3)
解:过点A作AE⊥BC与点E,并延长AE交直线CP与点D,如图所示.
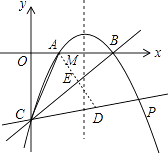
∵点A(2,0),点B(6,0),点O(0,0),点C(0,﹣6),
∴AB=4,OA=2,OC=6,OB=6.
由勾股定理可知:AC= ![]() =2
=2 ![]() ,BC=
,BC= ![]() =6
=6 ![]() ,
,
∴sin∠OBC= ![]() =
= ![]() =
= ![]() ,AE=2
,AE=2 ![]() .
.
∵∠PCB=∠ACB,且BC⊥AD,
∴CD=CA=2 ![]() ,DE=AE=2
,DE=AE=2 ![]() (等腰三角形三线合一),
(等腰三角形三线合一),
∴AD=AE+DE=4 ![]() .
.
设点D坐标为(m,n),
则由两点间的距离公式可知,
![]() ,解得
,解得  (舍去)或
(舍去)或 ![]() .
.
即此时点D的坐标为(6,﹣4).
设直线CP的解析式为y=k1x﹣6,将D点坐标代入得:
﹣4=6k1﹣6,解得:k1= ![]() .
.
∴若点P在抛物线上运动(点P异于点A),当∠PCB=∠BCA时,直线PC的解析式为y= ![]() x﹣6.
x﹣6.
【解析】(1)令x=0,可得点C坐标,令y=0,可得点A、B坐标,再结合三角形面积公式,即可得出结论;(2)找与直线BC平行且过动点P的直线,令此直线与抛物线相切,看切点P是否在x轴上方,如果在,则切点P到直线BC的距离就是所求最大距离,若不在,只需考虑端点A、B到直线BC的距离即可;(3)过点A作AE⊥BC与点E,并延长AE交直线CP与点D,巧妙利用等腰三角形的三线合一,找出AD、CD的长度,根据两点间的距离公式即可得出结论,不过此处要注意到会产生增根.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在出行中,主动采用能降低二氧化碳排放量的交通方式,谓之“低碳出行”.明明一家积极响应政府“绿色山城,低碳出行”的号召,今年2月﹣5月明明一家减少了驾车出行,他们将2月﹣5月驾车行驶的里程统计后绘制成以下两幅不完整的统计图:
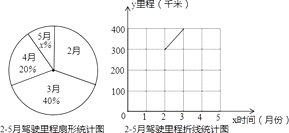
(1)扇形统计图中x= , 并补全折线统计图;
(2)某中学也积极参与“绿色山城,低碳出行”活动中,决定从4名广播社骨干成员中(其中两名男生,两名女生)选拔两名同学去演讲宣传,请用画树形图或列表的方法求所选出的两名同学恰好是一名男生一名女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证:

(1)EH=FH;
(2)∠CAB=2∠CDH. -
科目: 来源: 题型:
查看答案和解析>>【题目】《中华人民共和国道路交通管理条例》规定:小汽车在城街路上行驶速度不得超过70 km/h,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面车速检测仪 A的正前方60 m处的C点,过了5 s后,测得小汽车所在的B点与车速检测仪A之间的距离为100 m.
(1)求B,C间的距离.
(2)这辆小汽车超速了吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会为了解本校初中学生每天做作业所用时间情况,采用问卷的方式对一部分学生进行调查.在确定调查对象时,大家提出以下几种方案:A.对各班班长进行调查;B.对某班的全体学生进行调查;C.从全校每班随机抽取5名学生进行调查.在问卷调查时,每位被调查的学生都选择了问卷中适合自己的一个时间,学生会将收集到的数据整理后绘制成如图所示的条形统计图.
(1)为了使收集到的数据具有代表性.学生会在确定调查对象时应选择方案________ (填A,B或C);
(2)被调查的学生每天做作业所用时间的众数为________h;
(3)根据以上统计结果,估计该校900名初中学生中每天做作业用1.5 h的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次
第一档
第二档
第三档
每月用电量x(度)
0<x≤140
(2)小明家某月用电120度,需交电费 元
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
相关试题

