【题目】在出行中,主动采用能降低二氧化碳排放量的交通方式,谓之“低碳出行”.明明一家积极响应政府“绿色山城,低碳出行”的号召,今年2月﹣5月明明一家减少了驾车出行,他们将2月﹣5月驾车行驶的里程统计后绘制成以下两幅不完整的统计图: 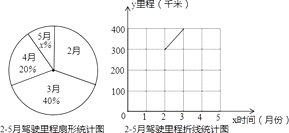
(1)扇形统计图中x= , 并补全折线统计图;
(2)某中学也积极参与“绿色山城,低碳出行”活动中,决定从4名广播社骨干成员中(其中两名男生,两名女生)选拔两名同学去演讲宣传,请用画树形图或列表的方法求所选出的两名同学恰好是一名男生一名女生的概率.
参考答案:
【答案】
(1)10
(2)解:设男生标记为A、B;女生标记为1、2,可能出现的所有结果列表如下:
A | B | 1 | 2 | |
A | / | (B,A) | (1,A) | (2,A) |
B | (A,B) | / | (1,B) | (2,B) |
1 | (A,1) | (B,1) | / | (2,1) |
2 | (A,2) | (B,2) | (1,2) | / |
共有12种可能的结果,且每种的可能性相同,其中刚好所选出的两名同学恰好是一名男生一名女生的结果有8种,
则P(一男一女)= ![]() =
= ![]() .
.
故答案为10
【解析】解:(1)∵3月驾车行驶400千米,占40%,
∴2月﹣5月驾车行驶的总里程数为:400÷40%=1000,
∴2月所占百分比为300÷1000=30%,
∴5月所占百分比为1﹣30%﹣40%﹣20%=10%,
∴x=10;
4月驾车行驶的里程数为:1000×20%=200,
5月驾车行驶的里程数为:1000×10%=100.
折线统计图补充如下: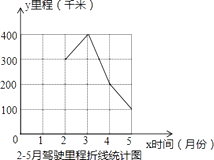
【考点精析】利用扇形统计图和折线统计图对题目进行判断即可得到答案,需要熟知能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,这是一个供滑板爱好者使用的U型池,该U型池可以看成是一个长方体去掉一个“半圆柱”,中间可供滑行部分的截面是半径为4 m的半圆,其边缘AB=CD=20 m,点E在CD上,CE=2 m.一滑板爱好者从A点滑到E点,则他滑行的最短路程约为____________(边缘部分的厚度忽略不计,结果保留整数.提示:482≈222).

-
科目: 来源: 题型:
查看答案和解析>>【题目】当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线顶点坐标为(1,3),且过点A(2,1).
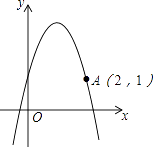
(1)求抛物线解析式;
(2)若抛物线与x轴两交点分别为点B、C,求线段BC的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证:

(1)EH=FH;
(2)∠CAB=2∠CDH. -
科目: 来源: 题型:
查看答案和解析>>【题目】《中华人民共和国道路交通管理条例》规定:小汽车在城街路上行驶速度不得超过70 km/h,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面车速检测仪 A的正前方60 m处的C点,过了5 s后,测得小汽车所在的B点与车速检测仪A之间的距离为100 m.
(1)求B,C间的距离.
(2)这辆小汽车超速了吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
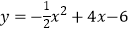 与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,
与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,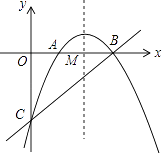
(1)求△ABC的面积;
(2)若p是x轴上方的抛物线上的一个动点,求点P到直线BC的距离的最大值;
(3)若点P在抛物线上运动(点P异于点A),当∠PCB=∠BCA时,求直线PC的解析式.
相关试题

