【题目】如图,A,B是两棵大树,两棵大树之间有一个废弃的圆形坑塘,为开发利用这个坑塘,需要测量A,B之间的距离,但坑塘附近地形复杂不容易直接测量.
(1)请你利用所学知识,设计一个测量A,B之间的距离的方案,并说明理由;
(2)在你设计的测量方案中,需要测量哪些数据?为什么?

参考答案:
【答案】(1)方案见解析,理由见解析;(2)见解析.
【解析】
(1)①如图,过点B作射线BD,在射线BD上选取O、D两点,使OD=OB;②连接OA,并延长OA至点C,使OC=OA;③连接CD,则CD的长即为AB的长.根据SAS证明△AOB≌△COD,由全等三角形的性质即可得AB=CD.(2)由(1)可知,这个方案需要测量5个数据,即:线段OA,OB,OC,OD,CD的长度,并使OC=OA,OD=OB,则CD=AB.
(1)方案为:①如图,过点B画一条射线BD,在射线BD上选取O、D两点,使OD=OB;
②连接OA,并延长OA至点C,使OC=OA;
③连接CD,则CD的长即为AB的长.
理由如下:在△AOB和△COD中,
∵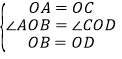 ,
,
∴△AOB≌△COD(SAS),
∴AB=CD.
(2)根据这个方案,需要测量5个数据,即:线段OA,OB,OC,OD,CD的长度,并使OC=OA,OD=OB,则CD=AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O在等边△ABC内,∠AOB=100°,∠BOC=x,将△BOC绕点C顺时针旋转60°,得△ADC,连接OD.
(1)△COD的形状是 ;
(2)当x=150°时,△AOD的形状是 ;此时若OB=3,OC=5,求OA的长;
(3)当x为多少度时,△AOD为等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=500,∠C=600,求∠DAE和∠BOA的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )cm.
A.4m
B.4n
C.2(m+n)
D.4(m﹣n) -
科目: 来源: 题型:
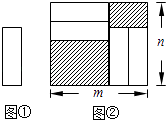
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小亮在学习探索三角形全等时,碰到如下一题:如图①,若AC=AD,BC=BD,则△ACB与△ADB有怎样的关系?

(1)请你帮他们解答,并说明理由;
(2)细心的小明在解答的过程中,发现如果在AB上任取一点E,连接CE,DE,则有CE=DE,你知道为什么吗(如图②)?
(3)小亮在小明说出理由后,提出如果在AB的延长线上任取一点P,也有(2)中类似的结论.请你帮他在图③中画出图形,并写出结论,不要求说明理由.
相关试题

