Question

【题目】小明和小亮在学习探索三角形全等时，碰到如下一题：如图①，若AC＝AD，BC＝BD，则△ACB与△ADB有怎样的关系？

(1)请你帮他们解答，并说明理由；

(2)细心的小明在解答的过程中，发现如果在AB上任取一点E，连接CE，DE，则有CE＝DE，你知道为什么吗(如图②)?

(3)小亮在小明说出理由后，提出如果在AB的延长线上任取一点P，也有(2)中类似的结论．请你帮他在图③中画出图形，并写出结论，不要求说明理由．

Answer 1

【答案】（1）见解析；（2）见解析；（3）PC=PD，图形见解析

【解析】

（1）根据全等三角形的判定定理SSS证得△ACB≌△ADB；

（2）由（1）中的全等三角形△ACB≌△ADB的对应角相等，得∠CAE=∠DAE，则由全等三角形的判定定理SAS证得△CAE≌△DAE，则对应边CE=DE；

（3）同（2），利用全等三角形的对应边相等证得结论．

（1）解：△ACB≌△ADB，理由如下：

如图1，∵在△ACB与△ADB中，

，

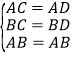∴△ACB≌△ADB（SSS），

（2）解：如图2，∵由（1）知，△ACB≌△ADB，

∴∠CAB=∠DAB，即∠CAE=∠DAE，

在△CAE与△DAE中，

，

∴△CAE≌△DAE（SAS），

∴CE=DE；

（3）解：如图3，PC=PD.

理由同（2），△APC≌△APD（SAS），

则PC=PD.