【题目】(11分)阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:32 39 45 55 60 54 60 28 56 41 51 36 44 46 40 53 37 47 45 46
(1)前10株西红柿秧上小西红柿个数的平均数是 ,中位数是 ,众数是 ;
(2)若对这20个数按组距8进行分组,请补全频数分布表及频数分布直方图:
个数分组 | 28≤x<36 | 36≤x<44 | 44≤x<52 | 52≤x<60 | 60≤x<68 |
频数 | 2 | 2 |
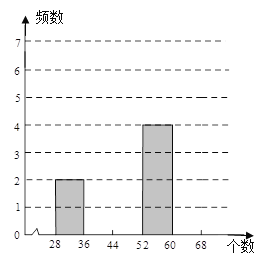
(3)通过频数分布直方图试分析此大棚中西红柿的长势。
参考答案:
【答案】(1)47;49.5;60.
详见解析;
(3)①此大棚的西红柿长势普遍较好,最少都有28个;
②西红柿个数最集中的株数在第三组,共有7株;
③西红柿的个数分布合理,中间多,两端少.(3条信息任答一条即可)
【解析】试题分析:(1)前10个数的平均数为(32+39+45+55+60+54+60+28+56+41)÷10=47;把这10个数从小到大排列后中间的两个数是45和54,所以这10个数的中位数是(45+54)÷2=49.5;这10个数中,60出现了2次,次数最多,是众数;(2)把这20个数据从小到大排列后,在28≤x<36范围内有28,32共2个数,因此频数是2;在36≤x<44范围内有36,37,39,40.41共5个数,因此频数是5;在44≤x<52范围内有44,45,45,46,46,47,51共7个数,因此频数是7;在52≤x<60范围内有53,54,55,56共4个数,因此频数是4;在60≤x<68范围内有60,60共2个数,因此频数是2.把对应的频数填入表格,并把频数分布直方图补全即可.(3)本题答案不唯一,只要符合要求即可.
试题解析:解:(1)47;49.5;60.
(2)
个数分组 | 28≤x<36 | 36≤x<44 | 44≤x<52 | 52≤x<60 | 60≤x<68 |
频数 | 2 | 5 | 7 | 4 | 2 |
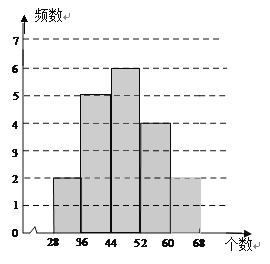
(3)①此大棚的西红柿长势普遍较好,最少都有28个;②西红柿个数最集中的株数在第三组,共有7株;③西红柿的个数分布合理,中间多,两端少.(3条信息任答一条,给满分2分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
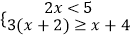 并在数轴上表示解集.
并在数轴上表示解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如表:
小组
研究报告
小组展示
答辩
甲
91
80
78
乙
81
74
85
丙
79
83
90
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某无人机于空中A处探测到目标B,D,从无人机A上看目标B,D的俯角分别为30°,60°,此时无人机的飞行高度AC为60m,随后无人机从A处继续飞行30
 m到达A′处,
m到达A′处,
(1)求A,B之间的距离;
(2)求从无人机A′上看目标D的俯角的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直线AD交于点A(
 ,
,  ),点D的坐标为(0,1)
),点D的坐标为(0,1) 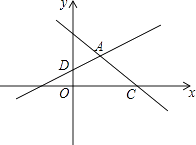
(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量(单位:吨),并将调查数据进行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
频数分布表
分组
划记
频数
2.0<x≤3.5
正正
11
3.5<x≤5.0

19
5.0<x≤6.5
6.5<x≤8.0
8.0<x≤9.5
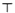
2
合计
50

(1)把上面频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可);
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=mx2+(1﹣2m)x+1﹣3m与x轴相交于不同的两点A、B
(1)求m的取值范围;
(2)证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;
(3)当 <m≤8时,由(2)求出的点P和点A,B构成的△ABP的面积是否有最值?若有,求出该最值及相对应的m值.
<m≤8时,由(2)求出的点P和点A,B构成的△ABP的面积是否有最值?若有,求出该最值及相对应的m值.
相关试题

