【题目】如下图,将边长为 9cm 的正方形纸片 ABCD 折叠,使得点 A 落在边 CD 上的 E 点,折痕为 MN.若 CE 的长为 6cm,则 MN 的长为_____cm.

参考答案:
【答案】3![]()
【解析】
根据图形折叠前后图形不发生大小变化得出∠MWE=∠AWM=90°,进而得出∠DAE=∠DAE,再证明△NFM≌△ADE,然后利用勾股定理的知识求出MN的长.
解:作NF⊥AD,垂足为F,连接AE,NE,
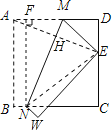
∵将正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN,
∴∠D=∠AHM=90°,∠DAE=∠DAE,
∴△AHM∽△ADE,
∴∠AMN=∠AED,
在△NFM和△ADE中
∵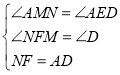 ,
,
∴△NFM≌△ADE(AAS),
∴FM=DE=CD-CE=3cm,
又∵在Rt△MNF中,FN=9cm,
∴根据勾股定理得:MN=![]() =3
=3![]() (cm).
(cm).
故答案为:3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体校要从四名射击选手中选拔一名参加省体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩
 及其方差S2如表所示:
及其方差S2如表所示:甲
乙
丙
丁
(环)
8.4
8.6
8.6
7.6
S2
0.74
0.56
0.94
1.92
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是( )
A.甲 B.乙 C.丙 D.丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,王老师布置如下任务:
如图1,△ABC中,BC>AB>AC,在BC边上取一点P,使∠APC=2∠ABC.
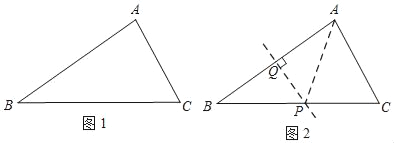
小路的作法如下,如图2:
①作AB边的垂直平分线,交BC于点P;
②连结AP.
所以,∠APC=2∠ABC.
小路的作图依据是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设有理数a、b、c满足a>b>c(ac<0),且|c|<|b|<|a|,则|x﹣
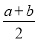 |+|x﹣
|+|x﹣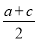 |+|x+
|+|x+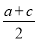 |的最小值是( )
|的最小值是( )A.
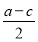 B.
B.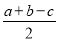 C.
C.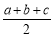 D.
D.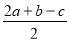
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等边三角形ABC的顶点B,C的坐标分别为(1,0),(3,0),过坐标原点O的一条直线分别与边AB,AC交于点M,N,若OM=MN,则点M的坐标为______________.
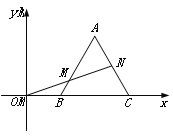
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=
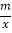 (m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
(m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.(1)求这两个函数的表达式;
(2)根据图象直接写出kx+b﹣
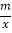 <0的x的取值范围.
<0的x的取值范围.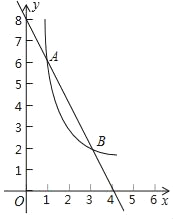
-
科目: 来源: 题型:
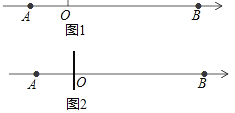
查看答案和解析>>【题目】如图1,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|a+4|+|b+3a|=0.
(1)求A、B两点之间的距离;
(2)若在数轴上存在一点C,且AC+BC=19,求C点表示的数;
(3)如图2,若在原点O处放一挡板,一小球甲从点A处以2个单位/秒的速度向左运动;两秒后另一个小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)乙球以4个单位/秒的速度向相反方向运动,设甲球运动的时间为t(秒).
①分别表示甲、乙两小球到原点的距离(用含t的式子表示);
②求甲、乙两小球到原点的距离相等时,甲球所在位置对应的数;
相关试题

