【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
(m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
(1)求这两个函数的表达式;
(2)根据图象直接写出kx+b﹣![]() <0的x的取值范围.
<0的x的取值范围.
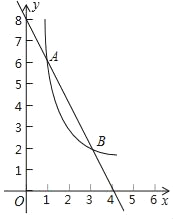
参考答案:
【答案】(1)y=﹣2x+8;(2)0<x<1或x>3
【解析】分析:(1)把A(1,6)代入反比例函数表达式,进而求得B点坐标,由A,B坐标和待定系数法可求得一次函数的解析式;
(2)观察图形,一次函数的值小于反比例函数的值,即在第一象限内,一次函数在反比例函数下面的部分.
详解:(1)∵把A(1,6)代入反比例函数表达式中,
m=1×6=6,
∴反比例函数表达式为:![]()
把B(3,n)代入得
n=2.
∴B(3,2),
把A(1,6),B(3,2)代入一次函数表达式,得
![]() 解得:
解得:![]()
∴一次函数表达式为:y=2x+8;
(2)有图象可知0<x<1或x>3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设有理数a、b、c满足a>b>c(ac<0),且|c|<|b|<|a|,则|x﹣
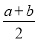 |+|x﹣
|+|x﹣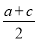 |+|x+
|+|x+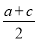 |的最小值是( )
|的最小值是( )A.
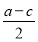 B.
B.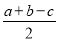 C.
C.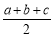 D.
D.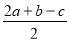
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,将边长为 9cm 的正方形纸片 ABCD 折叠,使得点 A 落在边 CD 上的 E 点,折痕为 MN.若 CE 的长为 6cm,则 MN 的长为_____cm.

-
科目: 来源: 题型:
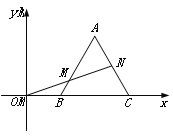
查看答案和解析>>【题目】如图,在平面直角坐标系中,等边三角形ABC的顶点B,C的坐标分别为(1,0),(3,0),过坐标原点O的一条直线分别与边AB,AC交于点M,N,若OM=MN,则点M的坐标为______________.
-
科目: 来源: 题型:
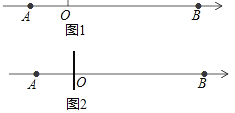
查看答案和解析>>【题目】如图1,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|a+4|+|b+3a|=0.
(1)求A、B两点之间的距离;
(2)若在数轴上存在一点C,且AC+BC=19,求C点表示的数;
(3)如图2,若在原点O处放一挡板,一小球甲从点A处以2个单位/秒的速度向左运动;两秒后另一个小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)乙球以4个单位/秒的速度向相反方向运动,设甲球运动的时间为t(秒).
①分别表示甲、乙两小球到原点的距离(用含t的式子表示);
②求甲、乙两小球到原点的距离相等时,甲球所在位置对应的数;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业原有管理人员与营销人员的人数之比为3∶2,总人数为150,为了扩大市场,从管理人员中抽调部分人员参加营销工作,就能使营销人员是管理人员的2倍,请问应从管理人员中抽调多少人参加营销工作?
-
科目: 来源: 题型:
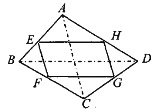
查看答案和解析>>【题目】如图,四边形 ABCD 中,E、F、G、H 分别为各边的中点,顺次连 结 E、F、G、H,把四边形 EFGH 称为中点四边形.连结 AC、BD,容易证明:中点 四边形 EFGH 一定是平行四边形.
(1)如果改变原四边形 ABCD 的形状,那么中点四边形的形状也随之改变,通过探索 可以发现:当四边形 AB CD 的对角线满足 AC=BD 时,四边形 EFGH 为菱形;当四边形ABCD 的对角线满足 时,四边形 EFGH 为矩形;当四边形 ABCD 的对角线满足 时,四边形 EFGH 为正方形.
(2)试证明:S△AEH+S△CFG=
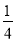 S□ ABCD
S□ ABCD(3)利用(2)的结论计算:如果四边形 ABCD 的面积为 2012, 那么中点四边形 EFGH 的面积是 (直接将结果填在 横线上)
相关试题

