【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O,与斜边AB交于点D、E为BC边的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)填空:①若∠B=30°,AC=2 ![]() ,则DE=;
,则DE=;
②当∠B=°时,以O,D,E,C为顶点的四边形是正方形.
参考答案:
【答案】
(1)
证明:连接OD.
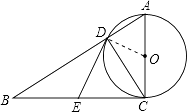
∵AC是直径,
∴∠ADC=90°,
∴∠CDB=90°,
又∵E为BC边的中点,
∴DE为直角△DCB斜边的中线,
∴DE=CE= ![]() .
.
∴∠DCE=∠CDE,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°,
∴∠ODE=90°
∴DE是⊙O的切线.
(2)3;45
【解析】(2)解:①∵∠B=30°,AC=2 ![]() ,∠BCA=90°,
,∠BCA=90°,
∴tan30°= ![]() =
= ![]() =
= ![]() ,
,
解得:BC=6,
则DE= ![]() BC=3;
BC=3;
故答案为:3;
②当∠B=45°时,四边形ODEC是正方形,
∵∠ACB=90°,
∴∠A=45°,
∵OA=OD,
∴∠ADO=45°,
∴∠AOD=90°,
∴∠DOC=90°,
∵∠ODE=90°,
∴四边形DECO是矩形,
∵OD=OC,
∴矩形DECO是正方形.
故答案为:45.
(1)运用垂径定理、直角三角形的性质证明∠ODE=90°即可解决问题;(2)①直接利用锐角三角函数关系得出BC的长,再利用直角三角形的性质得出DE的长;②当∠B=45°时,四边形ODEC是正方形,由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°然后根据有一组邻边相等的矩形是正方形,即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于与坐标轴不平行的直线l和点P,给出如下定义:过点P作x轴,y轴的垂线,分别交直线l于点M,N,若PM+PN≤4,则称P为直线l的近距点,特别地,直线上l所有的点都是直线l的近距点.已知点A(-
 ,0),B(0,2),C(-2,2).
,0),B(0,2),C(-2,2).(1)当直线l的表达式为y=x时,
①在点A,B,C中,直线l的近距点是 ;
②若以OA为边的矩形OAEF上所有的点都是直线l的近距点,求点E的纵坐标n的取值范围;
(2)当直线l的表达式为y=kx时,若点C是直线l的近距点,直接写出k的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是


A.
 ,
, B.
B.  ,
,
C.
 ,
, D.
D.  ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分
频数
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
n
80≤x<90
m
0.35
90≤x≤100
50
0.25
请根据所给信息,解答下列问题:
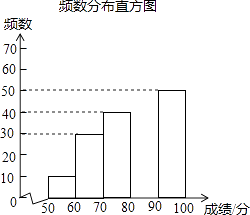
(1)m= , n=;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,不一定成立的是
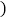
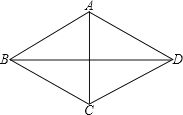
A. 四边形ABCD是平行四边形 B.
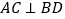
C.
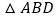 是等边三角形 D.
是等边三角形 D. 
-
科目: 来源: 题型:
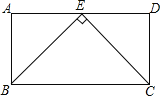
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD的中点,且
 若矩形ABCD的周长为48cm,则矩形ABCD的面积为______
若矩形ABCD的周长为48cm,则矩形ABCD的面积为______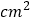 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校需要招聘一名教师,对三名应聘者进行了三项素质测试
 下面是三名应聘者的综合测试成绩:
下面是三名应聘者的综合测试成绩:应聘者
成绩
项目
A
B
C
基本素质
70
65
75
专业知识
65
55
50
教学能力
80
85
85
(1)如果根据三项测试的平均成绩确定录用教师,那么谁将被录用?
(2)学校根据需要,对基本素质、专业知识、教学能力的要求不同,决定按2:1:3的比例确定其重要性,那么哪一位会被录用?
相关试题

