【题目】一个铝质三角形框架三条边长分别为24cm、30cm、36cm,要估做一个与它相似的铝质三角形框架,现有长为27cm、45cm的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边.截法有( )
A.0种
B.1种
C.2种
D.3种
参考答案:
【答案】B
【解析】解:∵两根铝材的长分别为27cm、45cm,若45cm为一边时, 则另两边的和为27cm,27<45,不能构成三角形,
∴必须以27cm为一边,45cm的铝材为另外两边,
设另外两边长分别为x、y,则
①若27cm与24cm相对应时,![]() =
= ![]() =
= ![]() ,
,
解得:x=33.75cm,y=40.5cm,
x+y=33.75+40.5=74.25cm>45cm,故不成立;
②若27cm与36cm相对应时,![]() =
= ![]() =
= ![]() ,
,
解得:x=22.5cm,y=18cm,x+y=22.5+18=40.5cm<45cm,成立;
③若27cm与30cm相对应时,![]() =
= ![]() =
= ![]() ,
,
解得:x=32.4cm,y=21.6cm,x+y=32.4+21.6=54cm>45cm,故不成立;
故只有一种截法.
故选:B.
【考点精析】通过灵活运用相似三角形的应用,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
 的图形如图,以下结论: ①m<0;
的图形如图,以下结论: ①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a),点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.其中正确的个数是( )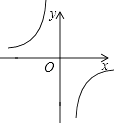
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,A点坐标为(10, 0),C点坐标为(0, 6),将边BC折叠,使点B落在边OA上的点D处,求线段EA 的长.
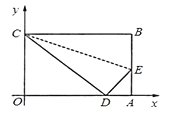
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 km.
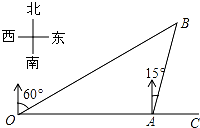
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点
 表示
表示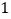 ,现将点
,现将点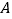 沿
沿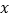 轴做如下移动,第一次点
轴做如下移动,第一次点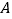 向左移动
向左移动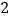 个单位长度到达点
个单位长度到达点 ,第二次将点
,第二次将点 ,向右移动
,向右移动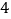 个单位长度到达点
个单位长度到达点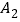 ,第三次将点
,第三次将点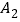 向左移动
向左移动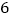 个单位长度到达点
个单位长度到达点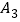 ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第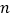 次移动到点
次移动到点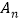 ,如果点
,如果点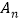 与原点的距离等于
与原点的距离等于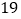 ,那么
,那么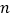 的值是________.
的值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH是什么四边形?证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? . (填一种即可)
相关试题

