搜索
【题目】如图，一个半径为r的圆形纸片在边长为a（ 
）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（ ）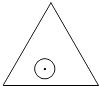
A.
B.
C.
D.πr2
参考答案：
【答案】C
【解析】如图，当圆形纸片运动到与
A的两边相切的位置时，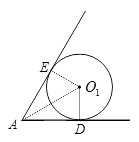
过圆形纸片的圆心O1作两边的垂线，垂足分别为D，E，
连接AO1，则Rt
ADO1中，O1AD=30
，O1D=r，AD=
r，
∴SADO1=
O1D
AD=
r2，由此S四边形ADO1E=2SADO1=r2，
∵由题意，DO1E=120，得S扇形O1DE=
r2，
∴圆形纸片“不能接触到的部分”的面积是3（r2-r2）=（
）r2 .
所以答案是：C.
【考点精析】认真审题，首先需要了解切线的性质定理(切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列美丽的图案，既是轴对称图形又是中心对称图形的个数是（ ）
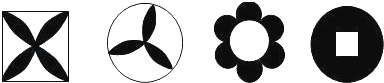
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】一个安装有进出水管的30升容器，水管单位时间内进出的水量是一定的，设从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，得到水量y（升）与时间x（分）之间的函数关系如图所示．根据图象信思给出下列说法，其中错误的是（ ）
A. 每分钟进水5升
B. 每分钟放水1.25升
C. 若12分钟后只放水，不进水，还要8分钟可以把水放完
D. 若从一开始进出水管同时打开需要24分钟可以将容器灌满
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABP与
是两个全等的等边三角形，且
，有下列四个结论：①
，②
，③
，④四边形ABCD是轴对称图形，其中正确的有
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，CA⊥AB，垂足为 A，AB＝24，AC＝12，射线 BM⊥AB，垂足为 B， 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动，点 D 为射线 BM 上一动点， 随着 E 点运动而运动，且始终保持 ED＝CB，当点 E 经过______秒时，△DEB 与△BCA 全等．
-
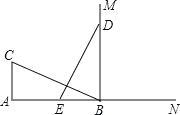
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知抛物线与直线的图象如图所示，当y1≠y2时，取y1 ， y2中的较大值记为N；当y1=y2时，N=y1=y2 ． 则下列说法：
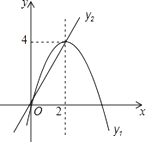
①当0＜x＜2时，N=y1；
②N随x的增大而增大的取值范围是x＜0；
③取y1 ， y2中的较小值记为M，则使得M大于4的x值不存在；
④若N=2，则x=2﹣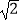
或x=1．
其中正确的有（ ）
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数的图象经过A（﹣1，4），B（1，﹣2）两点．
（1）求该一次函数的解析式；
（2）直接写出函数图象与两坐标轴的交点坐标．
相关试题
