【题目】已知一次函数的图象经过A(﹣1,4),B(1,﹣2)两点.
(1)求该一次函数的解析式;
(2)直接写出函数图象与两坐标轴的交点坐标.
参考答案:
【答案】(1)一次函数解析式为y=﹣3x+1;(2)一次函数与x轴的交点坐标为(![]() ,0),与y轴的交点坐标为(0,1).
,0),与y轴的交点坐标为(0,1).
【解析】
(1)利用待定系数法容易求得一次函数的解析式;
(2)分别令x=0和y=0,可求得与两坐标轴的交点坐标.
(1)设直线的解析式为y=kx+b.
∵图象经过点(﹣1,4),(1,﹣2)两点,∴把两点坐标代入函数解析式可得:![]() ,解得:
,解得:![]() ,∴一次函数解析式为y=﹣3x+1;
,∴一次函数解析式为y=﹣3x+1;
(2)在y=﹣3x+1中,令y=0,可得:﹣3x+1=0,解得:x![]() ;
;
令x=0,可得:y=1,∴一次函数与x轴的交点坐标为(![]() ,0),与y轴的交点坐标为(0,1).
,0),与y轴的交点坐标为(0,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个半径为r的圆形纸片在边长为a(
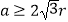 )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )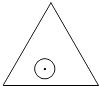
A.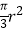
B.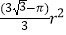
C.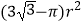
D.πr2 -
科目: 来源: 题型:
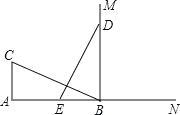
查看答案和解析>>【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1 , y2中的较大值记为N;当y1=y2时,N=y1=y2 . 则下列说法:
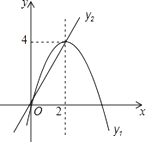
①当0<x<2时,N=y1;
②N随x的增大而增大的取值范围是x<0;
③取y1 , y2中的较小值记为M,则使得M大于4的x值不存在;
④若N=2,则x=2﹣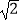 或x=1.
或x=1.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中二次函数解析式为y=ax2+bx+c(a≠0)则下列命题中正确的有(填序号).①abc>0;②b2<4ac;③4a﹣2b+c>0;④2a+b>c.
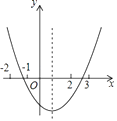
-
科目: 来源: 题型:
查看答案和解析>>【题目】杨华与季红用5张同样规格的硬纸片做拼图游戏,正面如图1所示,背面完全一样,将它们背面朝上搅匀后,同时抽出两张.规则如下:当两张硬纸片上的图形可拼成电灯或小人时,杨华得1分;当两张硬纸片上的图形可拼成房子或小山时,季红得1分(如图2).问题:游戏规则对双方公平吗?请说明理由;若你认为不公平,如何修改游戏规则才能使游戏对双方公平?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为 .
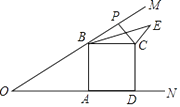
相关试题

