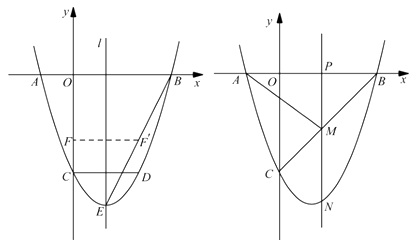
【题目】如图,二次函数 ![]() 的图像与
的图像与 ![]() 轴交于
轴交于 ![]() 、
、 ![]() 两点,与
两点,与 ![]() 轴交于点
轴交于点 ![]() ,
, ![]() .点
.点 ![]() 在函数图像上,
在函数图像上, ![]() 轴,且
轴,且 ![]() ,直线
,直线 ![]() 是抛物线的对称轴,
是抛物线的对称轴, ![]() 是抛物线的顶点.
是抛物线的顶点.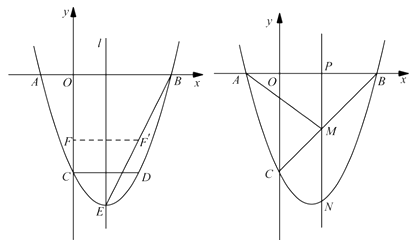
图 ① 图②
(1)求 ![]() 、
、 ![]() 的值;
的值;
(2)如图①,连接 ![]() ,线段
,线段 ![]() 上的点
上的点 ![]() 关于直线
关于直线 ![]() 的对称点
的对称点 ![]() 恰好在线段
恰好在线段 ![]() 上,求点
上,求点 ![]() 的坐标;
的坐标;
(3)如图②,动点 ![]() 在线段
在线段 ![]() 上,过点
上,过点 ![]() 作
作 ![]() 轴的垂线分别与
轴的垂线分别与 ![]() 交于点
交于点 ![]() ,与抛物线交于点
,与抛物线交于点 ![]() .试问:抛物线上是否存在点
.试问:抛物线上是否存在点 ![]() ,使得
,使得 ![]() 与
与 ![]() 的面积相等,且线段
的面积相等,且线段 ![]() 的长度最小?如果存在,求出点
的长度最小?如果存在,求出点 ![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
参考答案:
【答案】
(1)
解:∵CD⊥x轴,CD=2,
∴抛物线对称轴为直线l:x=1,
∴![]() =1,则b=-2。
=1,则b=-2。
∵OB=OC,C(0,c),
∴B点的坐标为(-c,0),
∴0=c2+2c+c,解得c=-3或c=0(舍去),
∴c=-3,
(2)
解:由(1)可得抛物线解析式为y=x2-2x-3,则E(1,-4)
设点F的坐标为(0,m),
∵对称轴为直线l:x=1,
∴点F关于直线l的对称点F的坐标为(2,m)。
∵直线BE经过点B(3,0),E(1,-4),
∴利用待定系数法可得直线BE的表达式y=2x-6,
∵点F在BE上,
∴m=2×2-6=-2,
即点F的坐标为(0,-2)。
(3)
解:存在点Q满足题意。设点P坐标为(n,0),则PA=n+1,PB=PM=3-n,PN=-n2+2n+3,
作QR⊥PN,垂足为R,
∵S△PQN=S△APM,
∴![]() (n+1)(3-n)=
(n+1)(3-n)=![]() (-n2+2n+3)QR,
(-n2+2n+3)QR,
∴QR=1。
①点Q在直线PN的左侧时,Q点的坐标为(n-1,n2-4n),R点的坐标为(n,n2-4n),N点的坐标为(n,n2-2n-3),
∴在Rt△QRN中,NQ2=1+(2n-3)2,
∴n=![]() 时,NQ取最小值1,此时Q点的坐标为(
时,NQ取最小值1,此时Q点的坐标为(![]() ,
,![]() )
)
②点Q在直线PN的右侧时,Q点的坐标为(n+1,n2-4).
同理NQ2=1+(2n-1)2,
∴n=![]() 时,NQ取最小值1,此时Q点的坐标为(
时,NQ取最小值1,此时Q点的坐标为(![]() ,
,![]() ).
).
综上所述,满足题意的点Q的坐标为(![]() ,
,![]() )和(
)和(![]() ,
,![]() )
)
【解析】(1)因为CD⊥x轴,所以C与D的纵坐标相等,即C与D关于抛物线的对称轴对称,则可得对称轴是直线l:x=1,从而由x=-![]() 代入a的值,求出b;又由OB=OC,可得B(-c,0),代入二次函数解析式,求出c的值即可;
代入a的值,求出b;又由OB=OC,可得B(-c,0),代入二次函数解析式,求出c的值即可;
(2)设点F的坐标为(0,m)关于直线x=1的对称点为(2,m),则求出BE的解析式,将(2,m)代入解出m的值即可;
(3)可设P(n,0),用n可表示出PA=n+1,PB=PM=3-n,PN=-n2+2n+3,作QR⊥PN,垂足为R,由S△PQN=S△APM , 可列出方程求出QR=1;
分类讨论点Q在直线PN的左侧和Q在直线PN的右侧时,在Rt△QRN中,由勾股定理可得NQ2=QR2+NR2,求出当n为多少时,NQ为最小值,写出相对应的Q的坐标。
【考点精析】掌握二次函数的图象和三角形的面积是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某教研机构为了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查.依据相关数据绘制成如图所示的不完整的统计图表,请根据图表中的信息解答下列问题:
某校初中生阅读数学教科书情况统计图表

类别
人数
占总人数比例
重视
a
0.3
一般
57
0.38
不重视
b
c
说不清楚
9
0.06
(1)求样本容量及表格中a,b,c的值,并补全统计图.
(2)若该校共有初中生2 300名,请估计该校“不重视阅读数学教科书”的初中生人数.
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式或不等式组,并把它们的解集在数轴上表示出来.
(1)5x+15>4x-13; (2)
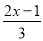 ≤
≤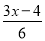 ;
;(3)
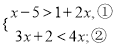 (4)
(4) 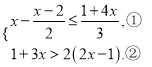
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC是等边三角形,点D、E分别是边BC、CA上的点,且BD=CE,AD、BE相交于点O.
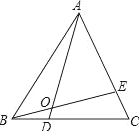
(1)求证:△BAE≌△ACD;
(2)求∠AOB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:(1)EC=BF;(2)EC⊥BF.
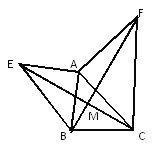
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年某区为绿化行车道,计划购买甲、乙两种树苗共计n棵.设购买甲种树苗x棵,有关甲、乙两种树苗的信息如图所示.
(1)当n=500时,
①根据信息填表(用含x的式子表示);
树苗类型
甲种树苗
乙种树苗
购买树苗数量(单位:棵)
x
购买树苗的总费用(单位:元)
②如果购买甲、乙两种树苗共用去25 600元,那么甲、乙两种树苗各购买了多少棵?
(2)要使这批树苗的成活率不低于92%,且使购买这两种树苗的总费用为26 000元,求n的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
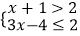 的解集表示在数轴上正确的是( )
的解集表示在数轴上正确的是( )
A.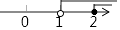
B.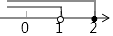
C.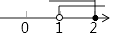
D.
相关试题

