【题目】已知不在同一条直线上的三点P,M,N 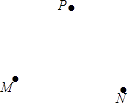
(1)画射线NP;再画直线MP;
(2)连接MN并延长MN至点R,使NR=MN;(保留作图痕迹,不写作图过程)
(3)若∠PNR比∠PNM大100°,求∠PNR的度数.
参考答案:
【答案】
(1)解:射线NP、直线MP如图所示
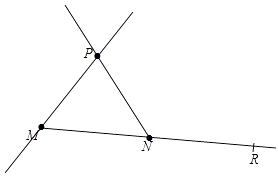
(2)解:连接MN并延长MN至点R,使NR=MN,点R即为舍弃(如图)

(3)解:∵∠PNR=∠PNM+100°,∠PNR+∠PNM=180°,
∴∠PNM+(∠PNM+100°)=180°,
∴2∠PNM=80°,
∴∠PNM=40°
【解析】(1)根据射线、直线的定义画出图形即可.(2)连接MN并延长MN至点R,截取NR=MN即可.(3)由题意可知∠PNR=∠PNM+100°,∠PNR+∠PNM=180°,即∠PNM+(∠PNM+100°)=180°,由此即可解决问题
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数
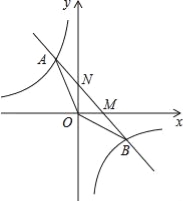
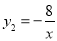 的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.(1)求一次函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出y1>y2时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程:计算:(﹣5)÷(
 ﹣
﹣  )×20 解:原式=(﹣5)÷(﹣
)×20 解:原式=(﹣5)÷(﹣  )×20 (第一步)
)×20 (第一步)
=(﹣5)÷(﹣4)(第二步)
=﹣20 (第三步)
(1)上述解题过程中有两处错误, 第一处是第步,错误的原因是;
第二处是第步,错误的原因是;
(2)把正确的解题过程写出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月20日上午8时,重庆国际马拉松赛在南滨路鸣枪开赛,来自30个国家和地区的3万多名跑者朝着快乐奔跑,最终埃塞俄比亚选手夺得男子组冠军,而女子全程前三名则由中国选手包揽.某校课外活动小组为了调查该校学生对“马拉松”喜爱的情况,随机对该校学生进行了调查,调查的结果分为“非常喜欢”、“比较喜欢”、“基本喜欢”、“不太喜欢”四个等级,分别记作A、B、C、D.根据调查结果绘制成了两幅不完整的统计图,请解答下列总量:
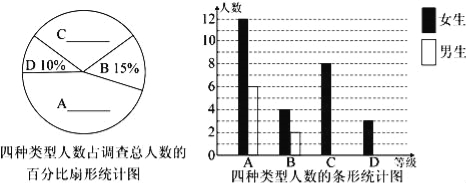
请你补全两种统计图并估算该校600名学生中“非常喜欢”马拉松的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列由四舍五入法得到近似数,各精确到哪一位:
0.0233;
3.10;
4.50万;
3.04×104; -
科目: 来源: 题型:
查看答案和解析>>【题目】盈盈超市第一次用6000元购进甲,乙两种商品,其中乙商品的件数比甲商品件数的
 多15件,甲,乙两种商品的进价和零售价如下表(注:获利=售价﹣进价):
多15件,甲,乙两种商品的进价和零售价如下表(注:获利=售价﹣进价): 甲
乙
进价(件/元)
22
30
售价(件/元)
29
40
(1)第一次进货时甲,乙两种商品各购进多少件?
(2)该超市第二次以第一次的进价又购进甲,乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍,甲商品按原价销售,乙商品打折销售.第二次两种商品都销售完后盈利2130元,求第二次乙种商品是按原价打几折销售的. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)a3﹣a2b+ab2+a2b﹣ab2+b2
(2)3(2x2﹣y2)﹣2(3y2﹣2x2)
相关试题

