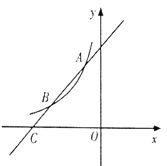
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数且
为常数且![]() )的图象交于
)的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求此反比例函数的表达式;
(2)若点![]() 在
在![]() 轴上,且
轴上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)反比例函数的表达式为![]() ;(2)点P(-6,0)或(-2,0).
;(2)点P(-6,0)或(-2,0).
【解析】(1)把点A(-1,a)代入![]() ,得
,得![]() ,得到A(-1,3),
,得到A(-1,3),
代入反比例函数![]() ,得
,得![]() ,即可求得反比例函数的表达式.
,即可求得反比例函数的表达式.
(2)联立两个函数表达式得 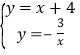 ,解得
,解得 ![]() ,
,![]() .求得点B的坐标,
.求得点B的坐标,
当![]() 时,得
时,得![]() .求得点C(-4,0). 设点P的坐标为(
.求得点C(-4,0). 设点P的坐标为(![]() ,0).根据
,0).根据![]() ,列出方程求解即可.
,列出方程求解即可.
【解答】(1)把点A(-1,a)代入![]() ,得
,得![]() ,
,
∴ A(-1,3)
把A(-1,3)代入反比例函数![]() ,得
,得![]() ,
,
∴ 反比例函数的表达式为![]() .
.
(2)联立两个函数表达式得 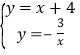 ,解得
,解得 ![]() ,
,![]() .
.
∴ 点B的坐标为B(-3,1).
当![]() 时,得
时,得![]() .
.
∴ 点C(-4,0).
设点P的坐标为(![]() ,0).
,0).
∵ ![]() ,
,
∴ ![]() .
.
即 ![]() ,
,
解得 ![]() ,
,![]() .
.
∴ 点P(-6,0)或(-2,0).
-
科目: 来源: 题型:
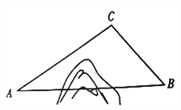
查看答案和解析>>【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,
 ,
,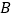 两地被大山阻隔,由
两地被大山阻隔,由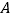 地到
地到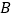 地需要绕行
地需要绕行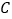 地,若打通穿山隧道,建成
地,若打通穿山隧道,建成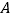 ,
,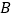 两地的直达高铁,可以缩短从
两地的直达高铁,可以缩短从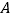 地到
地到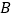 地的路程.已知:
地的路程.已知: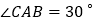 ,
,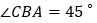 ,
,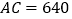 公里,求隧道打通后与打通前相比,从
公里,求隧道打通后与打通前相比,从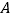 地到
地到 地的路程将约缩短多少公里?(参考数据:
地的路程将约缩短多少公里?(参考数据: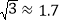 ,
,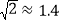 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形方格中,阴影部分是涂黑3个小正方形所形成的图案.
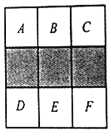
(1)如果将一粒米随机地抛在这个正方形方格上,那么米粒落在阴影部分的概率是多少?
(2)现将方格内空白的小正方形(
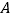 ,
,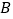 ,
, ,
,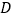 ,
, ,
, )中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率.
)中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率.四、解答题(二):本大题共5小题,共50分.解答应写出文字说明、证明过程或演算步骤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按
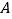 ,
, ,
,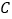 ,
,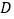 四个等级进行统计,制成了如下不完整的统计图.(说明:
四个等级进行统计,制成了如下不完整的统计图.(说明: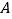 级:8分—10分,
级:8分—10分, 级:7分—7.9分,
级:7分—7.9分, 级:6分—6.9分,
级:6分—6.9分, 级:1分—5.9分)
级:1分—5.9分)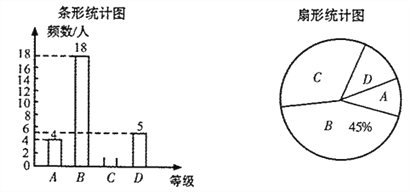
根据所给信息,解答以下问题:
(1)在扇形统计图中,
 对应的扇形的圆心角是_______度;
对应的扇形的圆心角是_______度;(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在_______等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到
 级的学生有多少人?
级的学生有多少人? -
科目: 来源: 题型:
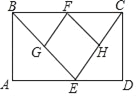
查看答案和解析>>【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车
乙种客车
载客量/(人/辆)
45
30
租金/(元/辆)
400
280
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
① (﹣21)+(﹣13)﹣(﹣25)﹣(+28)
② ﹣22﹣6÷(﹣2)×
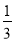
③先化简再求值:﹣a2b+(3ab2﹣a2b)﹣2(2ab2﹣a2b),其中 a=﹣1,b=﹣2.
(2)解下列方程
①x=1-(3 x-1)
②
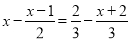
相关试题

