【题目】如图(1),PT与⊙O1相切于点T,PAB与⊙O1相交于A、B两点,可证明△PTA∽△PBT,从而有PT2=PAPB.请应用以上结论解决下列问题:如图(2),PAB、PCD分别与⊙O2相交于A、B、C、D四点,已知PA=2,PB=7,PC=3,则CD= . 
参考答案:
【答案】![]()
【解析】解:如图2中,过点P作⊙O的切线PT,切点是T. 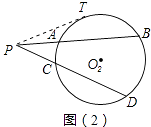
∵PT2=PAPB=PCPD,
∵PA=2,PB=7,PC=3,
∴2×7=3×PD,
∴PD= ![]()
∴CD=PD﹣PC= ![]() ﹣3=
﹣3= ![]() .
.
如图2中,过点P作⊙O的切线PT,切点是T,根据PT2=PAPB=PCPD,求出PD即可解决问题.本题考查相似三角形的判定和性质、切线的性质等知识,解题的关键是理解题意,学会利用新知解决未知,属于中考常考题型.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣
 ,y2)、点C(
,y2)、点C(  ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( ) 
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=
 BD,连接DM、DN、MN.若AB=6,则DN= .
BD,连接DM、DN、MN.若AB=6,则DN= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+4与双曲线y=
 (k≠0)相交于A(﹣1,a)、B两点,在y轴上找一点P,当PA+PB的值最小时,点P的坐标为 .
(k≠0)相交于A(﹣1,a)、B两点,在y轴上找一点P,当PA+PB的值最小时,点P的坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
①EF= OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=
OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=  OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=  ;⑤OGBD=AE2+CF2 .
;⑤OGBD=AE2+CF2 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣|﹣1|+
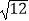 cos30°﹣(﹣
cos30°﹣(﹣  )﹣2+(π﹣3.14)0 .
)﹣2+(π﹣3.14)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生利用双休时间去距学校10km的炎帝故里参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.
相关试题

