【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
①EF= ![]() OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=
OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF= ![]() OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE= ![]() ;⑤OGBD=AE2+CF2 .
;⑤OGBD=AE2+CF2 . 
参考答案:
【答案】①②③⑤
【解析】解:①∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∴∠BOF+∠COF=90°,
∵∠EOF=90°,
∴∠BOF+∠COE=90°,
∴∠BOE=∠COF,
在△BOE和△COF中,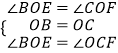 ,
,
∴△BOE≌△COF(ASA),
∴OE=OF,BE=CF,
∴EF= ![]() OE;故正确;
OE;故正确;
②∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC= ![]() S正方形ABCD ,
S正方形ABCD ,
∴S四边形OEBF:S正方形ABCD=1:4;故正确;
③∴BE+BF=BF+CF=BC= ![]() OA;故正确;
OA;故正确;
④过点O作OH⊥BC,
∵BC=1,
∴OH= ![]() BC=
BC= ![]() ,
,
设AE=x,则BE=CF=1﹣x,BF=x,
∴S△BEF+S△COF= ![]() BEBF+
BEBF+ ![]() CFOH=
CFOH= ![]() x(1﹣x)+
x(1﹣x)+ ![]() (1﹣x)×
(1﹣x)× ![]() =﹣
=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∵a=﹣ ![]() <0,
<0,
∴当x= ![]() 时,S△BEF+S△COF最大;
时,S△BEF+S△COF最大;
即在旋转过程中,当△BEF与△COF的面积之和最大时,AE= ![]() ;故错误;
;故错误;
⑤∵∠EOG=∠BOE,∠OEG=∠OBE=45°,
∴△OEG∽△OBE,
∴OE:OB=OG:OE,
∴OGOB=OE2 ,
∵OB= ![]() BD,OE=
BD,OE= ![]() EF,
EF,
∴OGBD=EF2 ,
∵在△BEF中,EF2=BE2+BF2 ,
∴EF2=AE2+CF2 ,
∴OGBD=AE2+CF2 . 故正确.
故答案为:①,②,③,⑤.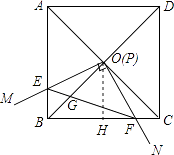
①由四边形ABCD是正方形,直角∠MPN,易证得△BOE≌△COF(ASA),则可证得结论;②由①易证得S四边形OEBF=S△BOC= ![]() S正方形ABCD , 则可证得结论;③由BE=CF,可得BE+BF=BC,然后由等腰直角三角形的性质,证得BE+BF=
S正方形ABCD , 则可证得结论;③由BE=CF,可得BE+BF=BC,然后由等腰直角三角形的性质,证得BE+BF= ![]() OA;④首先设AE=x,则BE=CF=1﹣x,BF=x,继而表示出△BEF与△COF的面积之和,然后利用二次函数的最值问题,求得答案;⑤易证得△OEG∽△OBE,然后由相似三角形的对应边成比例,证得OGOB=OE2 , 再利用OB与BD的关系,OE与EF的关系,即可证得结论.此题属于四边形的综合题.考查了正方形的性质,旋转的性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理以及二次函数的最值问题.注意掌握转化思想的应用是解此题的关键.
OA;④首先设AE=x,则BE=CF=1﹣x,BF=x,继而表示出△BEF与△COF的面积之和,然后利用二次函数的最值问题,求得答案;⑤易证得△OEG∽△OBE,然后由相似三角形的对应边成比例,证得OGOB=OE2 , 再利用OB与BD的关系,OE与EF的关系,即可证得结论.此题属于四边形的综合题.考查了正方形的性质,旋转的性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理以及二次函数的最值问题.注意掌握转化思想的应用是解此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=
 BD,连接DM、DN、MN.若AB=6,则DN= .
BD,连接DM、DN、MN.若AB=6,则DN= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+4与双曲线y=
 (k≠0)相交于A(﹣1,a)、B两点,在y轴上找一点P,当PA+PB的值最小时,点P的坐标为 .
(k≠0)相交于A(﹣1,a)、B两点,在y轴上找一点P,当PA+PB的值最小时,点P的坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),PT与⊙O1相切于点T,PAB与⊙O1相交于A、B两点,可证明△PTA∽△PBT,从而有PT2=PAPB.请应用以上结论解决下列问题:如图(2),PAB、PCD分别与⊙O2相交于A、B、C、D四点,已知PA=2,PB=7,PC=3,则CD= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣|﹣1|+
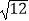 cos30°﹣(﹣
cos30°﹣(﹣  )﹣2+(π﹣3.14)0 .
)﹣2+(π﹣3.14)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生利用双休时间去距学校10km的炎帝故里参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40
请根据所给信息,解答下列问题:

(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
相关试题

