【题目】一个不透明的口袋中装有4个球,分别是红球和白球,这些球除颜色外都相同,将球搅匀,先从中任意摸出一个球,恰好摸到红球的概率为![]() .
.
(1)求口袋中有几个红球?
(2)先从中任意摸出一个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中一个是红球和一个是白球的概率.
参考答案:
【答案】(1)口袋里有2个红球;
(2)列表见解析,P(一个白球一个红球)![]() .
.
【解析】(1)设红球有x个,根据任意摸出一个球,恰好摸到红球的概率等于![]() ,求出x的值即可.
,求出x的值即可.
(2)列表得出所有等可能的情况数,找出两次摸到的球中一个是红球和一个是白球的情况数,即可求出所求的概率.
解:(1)4个小球中恰好摸到红球的概率等于![]() .
.
则![]() ,解得x=2个,即口袋里有2个红球;
,解得x=2个,即口袋里有2个红球;
(2)列表如下:
红 | 红 | 白 | 白 | |
红 | ﹣﹣﹣ | (红,红) | (白,红) | (白,红) |
红 | (红,红) | ﹣﹣﹣ | (白,红) | (白,红) |
白 | (红,白) | (红,白) | ﹣﹣﹣ | (白,白) |
白 | (红,白) | (红,白) | (白,白) | ﹣﹣﹣ |
所有等可能的情况有12种,其中两次摸到的球中一个是红球和一个是白球有8种可能,则P(一个白球一个红球)![]() .
.
“点睛”此题考查的是用列表法或树状法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适用于两步完成的事件;树状法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】六个正整数的中位数是4.5,众数是7,极差是6,这六个正整数的和为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①35=3×3×3×3×3;②﹣1是单项式,且它的次数为1;③若∠1=90°﹣∠2,则∠1与∠2互为余角;④对于有理数n、x、y(其中xy≠0),若
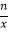 =
= 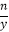 ,则x=y.其中不正确的有( )
,则x=y.其中不正确的有( )
A.3个
B.2个
C.1个
D.0个 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)5x﹣7=9﹣3x
(2)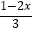 =
= 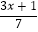 ﹣3.
﹣3. -
科目: 来源: 题型:
查看答案和解析>>【题目】解分式方程
 +
+  =3时,去分母后变形为( ).
=3时,去分母后变形为( ).
A.2+(x+2)=3(x﹣1)
B.2﹣x+2=3(x﹣1)
C.2﹣(x+2)=3(1﹣x)
D.2﹣(x+2)=3(x﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费.为更好地决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:

(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于两个不相等的实数a、b , 我们规定符号Max{a , b}表示a、b中的较大值,如:Max{2,4}=4,按照这个规定,方程Max{x , ﹣x}=
 的解为( ).
的解为( ).
A.1﹣
B.2﹣
C.1+ 或1﹣
或1﹣ 
D.1+ 或﹣1
或﹣1
相关试题

