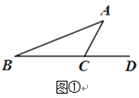
【题目】感知:如图①,∠ACD为△ABC的外角,易得∠ACD=∠A+∠B(不需证明) ;
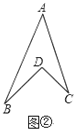
探究:如图②,在四边形ABDC中,试探究∠BDC与∠A、∠B.、∠C之间的关系,并说明理由;
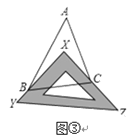
应用:如图③,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX=_______度;(直接填答案,不需证明)
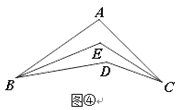
拓展:如图④,BE平分∠ABD,CE平分∠ACD,若∠BAC=100°,∠BDC=150°,则∠BEC=_______度. (直接填答案,不需证明)
参考答案:
【答案】 40 125
【解析】
(1)如图5,连接AD并延长至F,然后利用三角形外角的性质进行分析证明即可得到∠BDC=∠BAC+∠B+∠C;
(2)由题意可知∠BXC=90°,结合∠A=50°和(1)中所得结论即可得到∠ABX+∠ACX=90°-50°=40°;
(3)如图6,利用(1)中所得结论结合已知条件进行分析解答即可.
(1)如图5,连接AD并延长至点F.

∵∠BDF为△ABD的外角,
∴∠BDF=∠BAD+∠B,
同理可得∠CDF=∠CAD+∠C,
∴∠BDF+∠CDF=∠BAD+∠B+∠CAD+∠C,
即∠BDC=∠BAC+∠B+∠C;
(2)由题意可得∠BXC=90°,由(1)中结论可得∠BXC=∠A+∠ABX+∠ACX,
∵∠A=50°,
∴∠ABX+∠ACX=90°-50°=40°;
(3)如图6,∵∠A=100°,∠BDC=150°,∠BDC=∠A+∠ABD+∠ACD,
∴∠ABD+∠ACD=150°-100°=50°,
∵BE平分∠ABD,CE平分∠ACD,
∴∠ABE+∠ACE=![]() (∠ABD+∠ACD)=25°,
(∠ABD+∠ACD)=25°,
又∵∠BEC=∠A+∠ABE+∠ACE,
∴∠BEC=100°+25°=125°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把P’(y1,x1)叫做点P的友好点,已知点
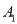 的友好点为
的友好点为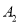 ,点
,点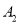 的友好点为
的友好点为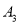 ,点
,点 的友好点为
的友好点为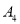 ,…,这样依次得到点.
,…,这样依次得到点.(1)当点
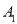 的坐标为(2,1),则点
的坐标为(2,1),则点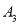 的坐标为___,点
的坐标为___,点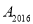 的坐标为___;
的坐标为___;(2)若
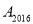 的坐标为(3,2),则设
的坐标为(3,2),则设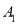 (x,y),求x+y的值;
(x,y),求x+y的值;(3)设点A1的坐标为(a,b),若
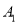 ,
,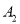 ,
,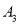 ,…
,…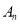 ,点
,点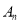 均在y轴左侧,求a、b的取值范围.
均在y轴左侧,求a、b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) (-4x2y)·(-x2y2)·(
 y)3; (2) (-3ab)(2a2b+ab-1) ;
y)3; (2) (-3ab)(2a2b+ab-1) ;(3) (m-
 )(m+
)(m+ ); (4) (-x-1)(-x+1) ; (5) ( - x - 5)2 ; (6)
); (4) (-x-1)(-x+1) ; (5) ( - x - 5)2 ; (6) ;
;(7)先化简,再求值:(x+1)2﹣(x+2)(x﹣2),其中
 ;
; (8)解方程组
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC=5,BC=6,点D是BC上的一点,那么点D到AB与AC的距离的和为( )
A.5
B.6
C.4
D.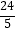
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,则(m﹣1)2+(n﹣1)2的最小值是( )
A.6
B.3
C.﹣3
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区规划在一个长30m、宽20m的长方形土地ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分钟花草,要使每一块花草的面积都为78cm2 , 那么通道宽应设计成多少m?设通道宽为xm,则由题意列得方程为( )

A.(30﹣x)(20﹣x)=78
B.(30﹣2x)(20﹣2x)=78
C.(30﹣2x)(20﹣x)=6×78
D.(30﹣2x)(20﹣2x)=6×78 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为 .

相关试题

