搜索
【题目】如图，AB是半圆O的直径，C是半圆O上一点，弦AD平分∠BAC，交BC于点E，若AB=6，AD=5，则DE的长为 ． 
参考答案：
【答案】
【解析】解：如图，连接BD，
∵AB为⊙O的直径，AB=6，AD=5，
∴∠ADB=90°，
∴BD= 
= 
，
∵弦AD平分∠BAC，
∴ 
，
∴∠DBE=∠DAB，
在△ABD和△BED中，
，
∴△ABD∽△BED，
∴ 
，即BD2=ED×AD，
∴（ ）2=ED×5，
解得DE= ．
所以答案是： ．
【考点精析】通过灵活运用勾股定理的概念和圆周角定理，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题．
-
科目： 来源： 题型：
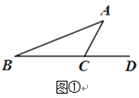
查看答案和解析>>【题目】感知：如图①，∠ACD为△ABC的外角，易得∠ACD=∠A+∠B(不需证明) ；
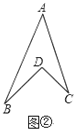
探究：如图②,在四边形ABDC中,试探究∠BDC与∠A、∠B.、∠C之间的关系，并说明理由；
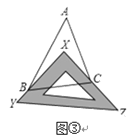
应用：如图③，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A=50°，则∠ABX+∠ACX=_______度；(直接填答案，不需证明)
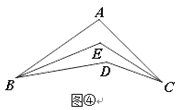
拓展：如图④，BE平分∠ABD，CE平分∠ACD，若∠BAC=100°，∠BDC=150°，则∠BEC=_______度. (直接填答案，不需证明)
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a≥2，m2﹣2am+2=0，n2﹣2an+2=0，则（m﹣1）2+（n﹣1）2的最小值是（ ）
A.6
B.3
C.﹣3
D.0 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某小区规划在一个长30m、宽20m的长方形土地ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分钟花草，要使每一块花草的面积都为78cm2 ， 那么通道宽应设计成多少m？设通道宽为xm，则由题意列得方程为（ ）
A.（30﹣x）（20﹣x）=78
B.（30﹣2x）（20﹣2x）=78
C.（30﹣2x）（20﹣x）=6×78
D.（30﹣2x）（20﹣2x）=6×78 -
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC中，∠A=90°，AB=AC ， BC=63cm，现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条，如图所示，已知剪得的纸条中有一张是正方形，则这张正方形纸条是从下往上数第张．
-
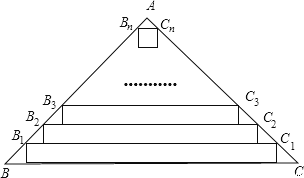
科目： 来源： 题型：
查看答案和解析>>【题目】特值验证：
当
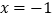，0，1，2，5，…时，计算代数式
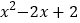的值，分别得到5，2，1，2，17，…．当x的取值发生变化时，代数式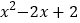的值却有一个确定的范围，通过多次验证可以发现它的值总大于或等于1，所以1就是它的最小值．变式求证：
我们可以用学过的知识，对
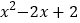进行恒等变形：
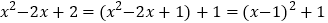．（注：这种变形方法可称为“配方”） 
，
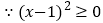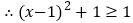．所以无论x取何值，代数式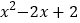的值不小于1，即最小值为1．迁移实证：
（1）请你用“配方”的方法，确定
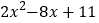的最小值为3；（2）求
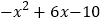的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF=
∠CAB．
（1）求证：直线BF是⊙O的切线；
（2）若AB=5，sin∠CBF=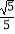
， 求BC和BF的长．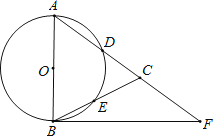
相关试题
